题目内容
13.如果△ABC∽△DEF,AB:DE=2:3,则S△ABC与S△DEF之比为$\frac{4}{9}$.分析 根据相似三角形的面积的比等于相似比的平方进行计算.
解答 解:∵△ABC∽△DEF,
∴S△ABC与S△DEF之比等于($\frac{AB}{DE}$)2=($\frac{2}{3}$)2=$\frac{4}{9}$.
故答案为:$\frac{4}{9}$.
点评 本题考查了相似三角形的性质:相似三角形的对应角相等,对应边的比相等;相似三角形的对应线段(对应中线、对应角平分线、对应边上的高)的比等于相似比;相似三角形的面积的比等于相似比的平方.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.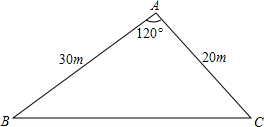 如图,有一块三角形空地需要开发,根据图中数据可知该空地的面积为( )
如图,有一块三角形空地需要开发,根据图中数据可知该空地的面积为( )
 如图,有一块三角形空地需要开发,根据图中数据可知该空地的面积为( )
如图,有一块三角形空地需要开发,根据图中数据可知该空地的面积为( )| A. | 100$\sqrt{3}m$2 | B. | 150$\sqrt{3}m$2 | C. | 200$\sqrt{3}m$2 | D. | 300$\sqrt{3}m$2 |
 如图,在正方形ABCD中,M为DC上一定点,N是AC上的一动点,要使DN+MN最小,请找出N点的位置.
如图,在正方形ABCD中,M为DC上一定点,N是AC上的一动点,要使DN+MN最小,请找出N点的位置.
 在A和B之间有一条河,在BA延长线上取一点C,作BC的垂线AD和CE,点D位于BE上,测得AC=5米,CE=3.3米,AD=3米,求AB之间的距离.这个问题源于古希腊海伦《Dioptra》中的间接测量问题.
在A和B之间有一条河,在BA延长线上取一点C,作BC的垂线AD和CE,点D位于BE上,测得AC=5米,CE=3.3米,AD=3米,求AB之间的距离.这个问题源于古希腊海伦《Dioptra》中的间接测量问题.