题目内容
18．
在A和B之间有一条河，在BA延长线上取一点C，作BC的垂线AD和CE，点D位于BE上，测得AC=5米，CE=3.3米，AD=3米，求AB之间的距离．这个问题源于古希腊海伦《Dioptra》中的间接测量问题．
分析 根据CE⊥BC，DA⊥BC可得出△ABD∽△CBE，再由相似三角形的对应边成比例即可得出结论．
解答 解：∵CE⊥BC，DA⊥BC，AC=5米，CE=3.3米，AD=3米，
∴△ABD∽△CBE，
∴$\frac{AD}{CE}$=$\frac{AB}{AC+AB}$，即$\frac{3}{3.3}$=$\frac{AB}{5+AB}$，
解得AB=50（米）．
点评 本题考查的是相似三角形的应用，熟知相似三角形的对应边成比例是解答此题的关键．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
如图，△ABC中，∠ACB=90°，AC=BC，D在BC上，BM⊥AD于M，求∠CMA的度数．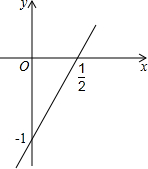
已知函数y=2x-1的图象如图所示，请根据图象回答下列问题：