题目内容
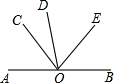 如图,已知A,O,B在一条直线上,OE平分∠BOD,∠COD=
如图,已知A,O,B在一条直线上,OE平分∠BOD,∠COD=| 1 |
| 2 |
考点:角平分线的定义
专题:
分析:首先设∠COD=x°,则∠AOC=2x°,根据角平分线的性质可得∠DOE=
∠DOB,再根据∠COE=72°,可得x°+
∠DOB=72°,然后再根据平角定义可得3x°+∠DOB=180°,计算出x的值,可得∠AOC的度数.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设∠COD=x°,则∠AOC=2x°,
∵OE平分∠BOD,
∴∠DOE=
∠DOB,
∵∠COE=72°,
∴x°+
∠DOB=72°,
∴2x°+∠DOB=144°,
∵3x°+∠DOB=180°,
∴x=36,
∴∠AOC=72°.
∵OE平分∠BOD,
∴∠DOE=
| 1 |
| 2 |
∵∠COE=72°,
∴x°+
| 1 |
| 2 |
∴2x°+∠DOB=144°,
∵3x°+∠DOB=180°,
∴x=36,
∴∠AOC=72°.
点评:此题主要考查了角平分线定义,关键是根据角之间的倍分关系列出方程.

练习册系列答案
相关题目
 如图,AC=
如图,AC=| 1 |
| 3 |
| 1 |
| 4 |
| A、1:6 | B、1:8 |
| C、1:12 | D、1:16 |
若∠A=12°12′,∠B=20°15′30″,∠C=20.25°,则( )
| A、∠A>∠B>∠C |
| B、∠B>∠C>∠A |
| C、∠A>∠C>∠B |
| D、∠C>∠A>∠B |
从O点看,射线OA在是北偏西60°方向上,射线OB在南偏东15°方向上,那么∠AOB的度数为( )
| A、45° | B、75° |
| C、90° | D、135° |
 △ABC中,AB⊥BC,AB=BC,E为BC上一点,连接AE,过点C作CF⊥AE交AE的延长线于点F,连接BF,过点B作BG⊥BF交AE于G.
△ABC中,AB⊥BC,AB=BC,E为BC上一点,连接AE,过点C作CF⊥AE交AE的延长线于点F,连接BF,过点B作BG⊥BF交AE于G.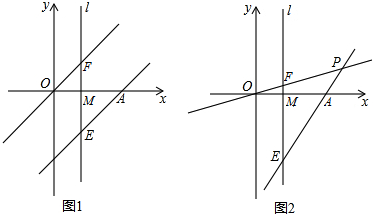
 如图,AB、CD交于点O,∠AOE=90°,若∠AOC:∠COE=5:4,求∠AOD的度数.
如图,AB、CD交于点O,∠AOE=90°,若∠AOC:∠COE=5:4,求∠AOD的度数.