题目内容
 如图,一个边长为4cm的等边三角形ABC与⊙O等高,⊙O与BC相切于点C,⊙O与AC相交于点D,则阴影部分的面积为
如图,一个边长为4cm的等边三角形ABC与⊙O等高,⊙O与BC相切于点C,⊙O与AC相交于点D,则阴影部分的面积为考点:扇形面积的计算,等边三角形的性质,切线的性质
专题:
分析:过点A作AE⊥BC于点E,过点O作OF⊥AC于点F,根据等腰三角形的性质求出AE的长,由三角形ABC与⊙O等高即可得出圆的半径,再根据⊙O与BC相切于点C可知OC⊥BC,故可得出∠OCD的度数,由三角形内角和定理求出∠COD的度数,根据直角三角形的性质求出OF及CF的长,由S阴影=S扇形-S△OCD即看得出结论.
解答: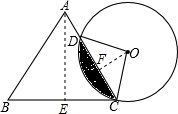 解:过点A作AE⊥BC于点E,过点O作OF⊥AC于点F,
解:过点A作AE⊥BC于点E,过点O作OF⊥AC于点F,
∵△ABC是等边三角形,AB=4,
∴AE=AB•sin60°=4×
=2
(cm).
∵等边三角形ABC与⊙O等高,
∴OD=
.
∵⊙O与BC相切于点C,
∴OC⊥BC,
∴∠OCD=90°-60°=30°.
∵OD=OC,
∴∠COD=180°-30°-30°=120°,
∴OF=
OC=
,CF=OC•cos30°=
×
=
,
∴CD=2CF=3,
∴S阴影=S扇形-S△OCD=
-
×3×
=(π-
)cm2.
故答案为:π-
.
 解:过点A作AE⊥BC于点E,过点O作OF⊥AC于点F,
解:过点A作AE⊥BC于点E,过点O作OF⊥AC于点F,∵△ABC是等边三角形,AB=4,
∴AE=AB•sin60°=4×
| ||
| 2 |
| 3 |
∵等边三角形ABC与⊙O等高,
∴OD=
| 3 |
∵⊙O与BC相切于点C,
∴OC⊥BC,
∴∠OCD=90°-60°=30°.
∵OD=OC,
∴∠COD=180°-30°-30°=120°,
∴OF=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
∴CD=2CF=3,
∴S阴影=S扇形-S△OCD=
120π×(
| ||
| 360 |
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 4 |
故答案为:π-
3
| ||
| 4 |
点评:本题考查的是扇形面积的计算,熟知等腰三角形的性质及扇形的面积公式是解答此题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
若∠A=12°12′,∠B=20°15′30″,∠C=20.25°,则( )
| A、∠A>∠B>∠C |
| B、∠B>∠C>∠A |
| C、∠A>∠C>∠B |
| D、∠C>∠A>∠B |
 如图,数轴A、B上两点分别对应实数a、b,则下列结论正确的是( )
如图,数轴A、B上两点分别对应实数a、b,则下列结论正确的是( )| A、a+b>0 | ||||
| B、ab=0 | ||||
C、
| ||||
D、
|
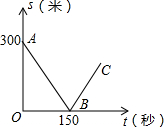 甲、乙两名自行车爱好者准备在一段长为3500米的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面.他们同时出发,匀速前进,已知甲的速度为12米/秒,设甲、乙两人之间的距离为s(米),比赛时间为t(秒),图中的折线表示从两人出发至其中一人先到达终点的过程中s(米)与t(秒)的函数关系.根据图中信息,回答下列问题:
甲、乙两名自行车爱好者准备在一段长为3500米的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面.他们同时出发,匀速前进,已知甲的速度为12米/秒,设甲、乙两人之间的距离为s(米),比赛时间为t(秒),图中的折线表示从两人出发至其中一人先到达终点的过程中s(米)与t(秒)的函数关系.根据图中信息,回答下列问题: 如图,△ABC的中线AE,BD相交于点G,DF∥BC交AE于点F,求
如图,△ABC的中线AE,BD相交于点G,DF∥BC交AE于点F,求 直线AB、CD、EF都经过点O且AB⊥CD,OG平分∠BOE,如果∠EOG=
直线AB、CD、EF都经过点O且AB⊥CD,OG平分∠BOE,如果∠EOG=