题目内容
2.在直角坐标平面中,O为坐标原点,二次函数y=-x2+(k-1)x+3的图象与y轴交于点A,与x轴交于点B,C(点B在负半轴),且S△OAB=$\frac{9}{2}$.(1)求点B的坐标;
(2)求此二次函数的解析式;
(3)在线段AB上取点P,过P作y轴的平行线,与抛物线交于点Q,试求线段PQ取得最大或最小值时点P的坐标.
分析 (1)根据三角形面积公式求出OB即可解决问题.
(2)把点B坐标代入y=-x2+(k-1)x+3即可.
(3)设点P(a,a+3),则Q(a,-a2-2a+3),PQ=-a2-2a+3-(a+3)=-a2-3a利用二次函数的性质即可解决问题.
解答 解:(1)由题意点A(0,3),设点B坐标为(m,0)(m<0),
∵$\frac{1}{2}$•(-m)•3=$\frac{9}{2}$,
∴m=-3,
∴点B坐标为(-3,0).
(2)把点B坐标代入y=-x2+(k-1)x+3得0=-9-3k+3+3,k=-1,
∴二次函数解析式为y=-x2-2x+3.
(3)∵直线AB为y=x+3,
设点P(a,a+3),则Q(a,-a2-2a+3),
PQ=-a2-2a+3-(a+3)=-a2-3a=-(x+$\frac{3}{2}$)2+$\frac{9}{4}$,
∴当x=-$\frac{3}{2}$时,PQ最大值=$\frac{9}{4}$,
此时点P坐标(-$\frac{3}{2}$,$\frac{3}{2}$).
点评 本题考查抛物线与x轴交点有关的知识、二次函数的性质、最值问题等知识,熟练掌握待定系数法确定函数解析式,解题的关键是利用二次函数的性质解决最值问题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
17.计算(3a)-1的结果是( )
| A. | $\frac{3}{a}$ | B. | $\frac{1}{3a}$ | C. | 3a | D. | $\frac{a}{3}$ |
 如图,在△ABC中,BD是中线,且BD=$\frac{1}{2}$AC,求证:∠ABC=90°.
如图,在△ABC中,BD是中线,且BD=$\frac{1}{2}$AC,求证:∠ABC=90°.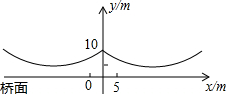 如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,右面的一条抛物线可以用y=0.0225x2+0.9x+10 表示,而且左、右两条抛物线关于y轴对称.
如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,右面的一条抛物线可以用y=0.0225x2+0.9x+10 表示,而且左、右两条抛物线关于y轴对称.