题目内容
13.y=$\sqrt{2-x}+\sqrt{x-2}+{x}^{2}+5$,求yx的平方根和算术平方根.分析 根据二次根式有意义可得$\left\{\begin{array}{l}{2-x≥0}\\{x-2≥0}\end{array}\right.$,再解不等式组可得x的值,代入y=$\sqrt{2-x}+\sqrt{x-2}+{x}^{2}+5$可得y的值,然后再计算出yx=81,再求平方根和算术平方根即可.
解答 解:由题意得:$\left\{\begin{array}{l}{2-x≥0}\\{x-2≥0}\end{array}\right.$,
解得:x=2,
则y=4+5=9,
yx=81,
81平方根±9,算术平方根是9.
点评 此题主要二次根式有意义的条件,以及算术平方根和平方根,关键是掌握二次根是的被开方数为非负数正确确定x、y的值.

练习册系列答案
相关题目
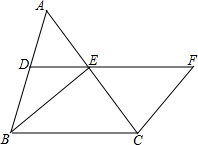 如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到F,使EF=BE,连接CF.
如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到F,使EF=BE,连接CF.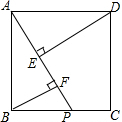 如图,正方形ABCD中,点P在BC边上,DE⊥AP于点E,BF⊥AP于点F,若BF=x,DE=y,EF=2,求y与x的函数关系式,并画出函数图象.
如图,正方形ABCD中,点P在BC边上,DE⊥AP于点E,BF⊥AP于点F,若BF=x,DE=y,EF=2,求y与x的函数关系式,并画出函数图象. 如图,
如图,