题目内容
9.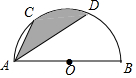 如图,AB为半圆O的直径,C,D为半圆弧的三等分点,若AB=12,则阴影部分的面积为6π.
如图,AB为半圆O的直径,C,D为半圆弧的三等分点,若AB=12,则阴影部分的面积为6π.
分析 连接OC、OD、CD,利用同底等高的三角形面积相等可知阴影部分的面积等于扇形OCD的面积,然后计算扇形面积就可.
解答 解:连接OC、OD、CD.
∵△COD和△CPD等底等高,
∴S△COD=S△POD.
∵点C,D为半圆的三等分点,
∴∠COD=180°÷3=60°,
∴阴影部分的面积=S扇形COD=$\frac{60•π•{6}^{2}}{360}$=6π,
故答案为:6π.
点评 本题主要考查扇形面积的计算,解题的关键是理解阴影部分的面积等于扇形OCD的面积.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
19.函数y=$\frac{\sqrt{x}}{{x}^{2}+2}$-x0的自变量的取值范围是( )
| A. | x≥0 | B. | x>0且x≠-2 | C. | x≥0且x≠-2 | D. | x>0 |
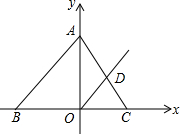 如图,在平面直角坐标系中,已知点A在y轴的正半轴上,点B、点C分别在x轴的负半轴和正半轴上,OB、OC的长分别是方程x2-5x+6=0的两根(OB>OC),△ABC为等腰三角形,且AB=BC.
如图,在平面直角坐标系中,已知点A在y轴的正半轴上,点B、点C分别在x轴的负半轴和正半轴上,OB、OC的长分别是方程x2-5x+6=0的两根(OB>OC),△ABC为等腰三角形,且AB=BC. 如图,已知∠DOE=67°,OD平分∠AOC,OE平分∠BOC,求∠AOB度数.
如图,已知∠DOE=67°,OD平分∠AOC,OE平分∠BOC,求∠AOB度数.