题目内容
9.(1)计算:${(-1)^{2012}}+tan6{0°}-|{1-\sqrt{3}}|+{(3.14-π)^0}$(2)解分式方程:$\frac{2-x}{x-3}+\frac{1}{3-x}=1$.
分析 (1)分别利用绝对值以及零指数幂的性质和特殊角的三角函数值化简求出即可;
(2)首先去分母进而解方程,最后检验即可.
解答 解:(1)${(-1)^{2012}}+tan6{0°}-|{1-\sqrt{3}}|+{(3.14-π)^0}$
=1+$\sqrt{3}$-($\sqrt{3}$-1)+1
=1+$\sqrt{3}$-$\sqrt{3}$+1+1
=3;
(2)$\frac{2-x}{x-3}+\frac{1}{3-x}=1$
去分母得:
2-x-1=x-3,
解得:x=2,
检验:当x=2时,x-3≠0,
故x=2是原方程的根.
点评 此题主要考查了特殊角的三角函数值以及绝对值以及零指数幂的性质和分式方程的解法,正确解分式方程是解题关键.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 如图,已知OP平分∠AOB,过点P作OP的垂线分别交OA、OB于点C、D,请问:PC=PD吗?为什么?能不能利用角平分线的性质求证呢?
如图,已知OP平分∠AOB,过点P作OP的垂线分别交OA、OB于点C、D,请问:PC=PD吗?为什么?能不能利用角平分线的性质求证呢? 如图所示,在△ABC中,∠A=36°,且∠ABC=∠C,BD是△ABC的高.试求∠C与∠DBC的度数.
如图所示,在△ABC中,∠A=36°,且∠ABC=∠C,BD是△ABC的高.试求∠C与∠DBC的度数.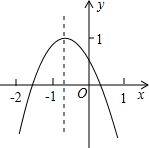 二次函数y=ax2+bx+c(a≠0)的图象如图所示,若M=a+b+c,N=a-c,P=-$\frac{b}{2a}$,则在M,N,P中,值小于0的数有( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,若M=a+b+c,N=a-c,P=-$\frac{b}{2a}$,则在M,N,P中,值小于0的数有( )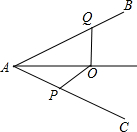 如图,AO是∠BAC的平分线,P、Q分别是AC、AB边上的点,若∠OQB+∠OPC=180°,此时OP与OQ会相等吗?若相等请证明,不相等请说明理由.
如图,AO是∠BAC的平分线,P、Q分别是AC、AB边上的点,若∠OQB+∠OPC=180°,此时OP与OQ会相等吗?若相等请证明,不相等请说明理由.