题目内容
16. 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,2)、B(4,5)、C(-2,-1).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,2)、B(4,5)、C(-2,-1).(1)在平面直角坐标系中描出点A、B、C,求△ABC的面积;
(2)x轴上是否存在点P,使△ACP的面积为4,如果存在,求出点P的坐标,如果不存在,说明理由.y轴上存在点Q,使△ACQ的面积为4吗?如果存在,求出点Q的坐标,如果不存在,说明理由;
(3)如果以点A为原点,以经过点A平行于x轴的直线为x′轴,向右的方向为x′轴的正方向;以经过点A平行于y轴的直线为y′轴,向上的方向为y′轴的正方向;单位长度相同,建立新的直角坐标系,直接写出点B、点C在新的坐标系中的坐标.
分析 (1)根据三点的坐标,在直角坐标系中分别标出位置可描出点A、B、C,把AC当作底,点B到AC的距离当作高,根据三角形的面积公式计算即可得出△ABC的面积;
(2)设AC与x轴交于点M,则M(-2,0).根据△ACP的面积为4,求出PM=$\frac{8}{3}$,进而求得点P的坐标;由于y轴上任意一点与AC的距离都是2,根据三角形的面积公式得出:当点Q在y轴上时,△ACQ的面积=$\frac{1}{2}$×3×2=3≠4,即可说明y轴上不存在点Q,使△ACQ的面积为4;
(3)根据条件画出新的直角坐标系,即可写出点B、点C在新的坐标系中的坐标.
解答 解:(1)如图所示: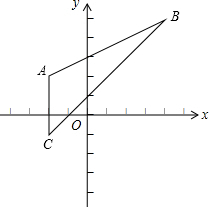
∵A(-2,2)、B(4,5)、C(-2,-1),
∴△ABC的面积=$\frac{1}{2}$×3×6=9;
(2)x轴上存在点P,使△ACP的面积为4.理由如下: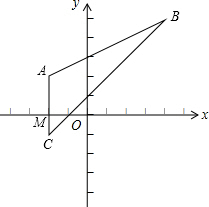
设AC与x轴交于点M,则M(-2,0).
∵△ACP的面积为4,
∴$\frac{1}{2}$AC•PM=$\frac{1}{2}$×3×PM=4,
∴PM=$\frac{8}{3}$,
∴点P的坐标为(-$\frac{14}{3}$,0)或($\frac{2}{3}$,0);
y轴上不存在点Q,使△ACQ的面积为4.理由如下:
∵AC∥y轴,y轴上任意一点与AC的距离都是2,
∴当点Q在y轴上时,△ACQ的面积=$\frac{1}{2}$×3×2=3≠4,
∴y轴上不存在点Q,使△ACQ的面积为4;
(3)如图所示:
在新的直角坐标系中,点B的坐标为(6,3),点C的坐标为(0,-3).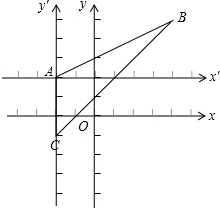
点评 本题考查了坐标与图形性质,三角形的面积,难度一般,解答本题的关键是正确作图,利用数形结合的思想.

练习册系列答案
相关题目
11.随着人民生活水平提高,环境污染问题日趋严重,为了更好治理和净化河道,保护环境,河道综合治理指挥部决定购买10台污水处理设备.现有A、B两种型号的设备,其中每台的价格、月处理污水量如表.经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求表中a,b的值;
(2)由于受资金限制,河道综合治理指挥部决定购买污水处理设备的资金不超过110万元,问每月最多能处理污水多少吨?
| A型 | B型 | |
| 价格(万元/台) | a | b |
| 处理污水量(吨/月) | 220 | 180 |
(2)由于受资金限制,河道综合治理指挥部决定购买污水处理设备的资金不超过110万元,问每月最多能处理污水多少吨?
 如图,已知∠1+∠3=180°,请说明a∥b.
如图,已知∠1+∠3=180°,请说明a∥b. 在?ABCD中,对角线AC,BD相交于点O,点E,F在AC上且AE=CF,
在?ABCD中,对角线AC,BD相交于点O,点E,F在AC上且AE=CF, 如图,A、B两点的坐标分别为(2,4),(6,0),点P是x轴上一点,且△ABP的面积为6,则点P的坐标为(3,0)或(9,0).
如图,A、B两点的坐标分别为(2,4),(6,0),点P是x轴上一点,且△ABP的面积为6,则点P的坐标为(3,0)或(9,0).