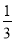��Ŀ����
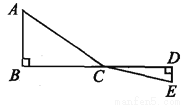
��ͼ��CΪ�߶�BD��һ���㣬�ֱ����B��D��AB��BD��ED��BD������AC��EC����֪AB=5��DE=1��BD=8����CD=x��
(1)�ú�x�Ĵ���ʽ��ʾAC+CE�ij���
(2)���ʵ�C����ʲô����ʱ��AC+CE��ֵ��С���������Сֵ��
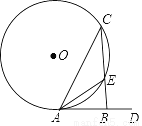
(3)����(2)�еĹ��ɺͽ��ۣ��빹ͼ�������ʽ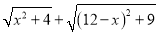 ����Сֵ��
����Сֵ��
��ϰ��ϵ�д�
 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�
�����Ŀ
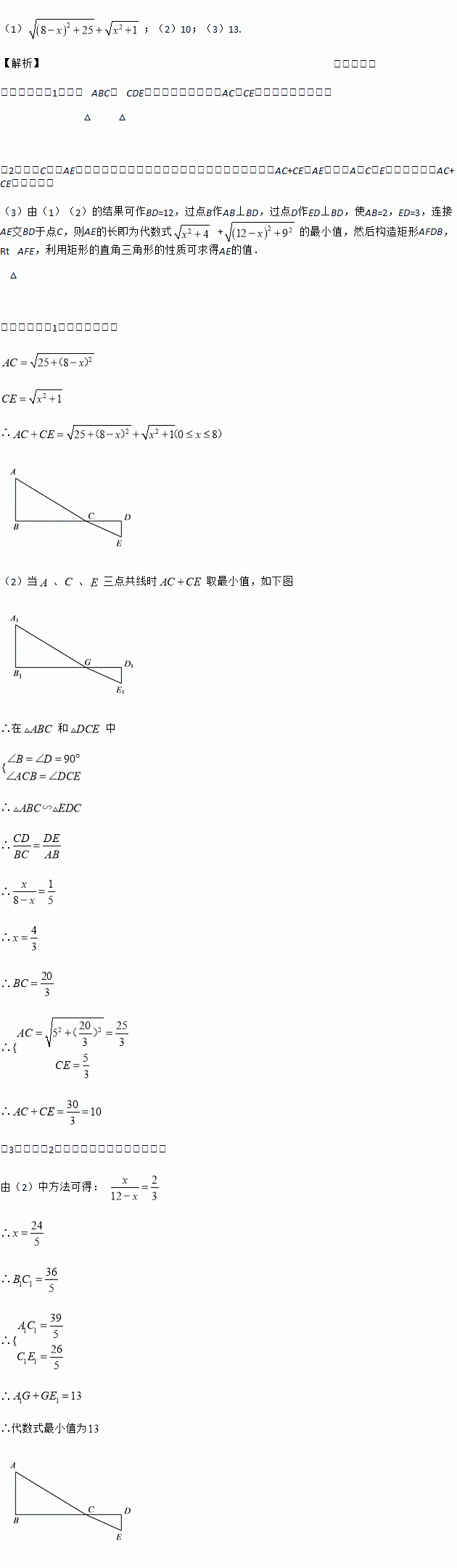

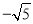 ���෴����_____��ƽ������
���෴����_____��ƽ������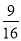 ������_____���ֽ���ʽ��a3��a=_____��
������_____���ֽ���ʽ��a3��a=_____�� ������ǰ15�����ķ��ӡ���ĸ�Ĺ��ɹ���������ȥ����100�����ǣ�������
������ǰ15�����ķ��ӡ���ĸ�Ĺ��ɹ���������ȥ����100�����ǣ�������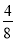 B.
B.  C.
C. 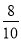 D.
D. 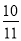
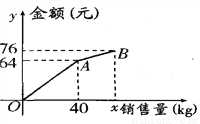
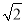 �����B����ʾ����Ϊm����
�����B����ʾ����Ϊm����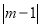 +(m+6)��ֵΪ ( )
+(m+6)��ֵΪ ( )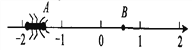
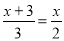 ʱ,ȥ��ĸ����Եõ�(��)
ʱ,ȥ��ĸ����Եõ�(��)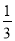
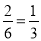 .
.