题目内容
已知矩形ABCD的对角线AC,BD的长度是关于x的方程x2-px+p+3=0的两个实数根,则此矩形面积的最大值是 .
考点:矩形的性质,根的判别式
专题:
分析:根据矩形性质求出AC=BD,根据根的判别式求出P,求出AC、BD的值,根据完全平方公式得出S≤
AC×BD,代入求出即可.
| 1 |
| 2 |
解答:解:∵四边形ABCD是矩形,
∴AC=BD,
∵矩形ABCD的对角线AC,BD的长度是关于x的方程x2-px+p+3=0的两个实数根,
∴△=p2-4×1×(p+3)=0,
解得:p1=6,p2=-2(不符合题意,舍去),
则方程为x2-6x+9=0,
即AC=BD=3,
由勾股定理得:AB2+BC2=AC2=9,
∵S=
AC×BD,
∴S≤
AC×BD=
,
故答案为:
.

∴AC=BD,
∵矩形ABCD的对角线AC,BD的长度是关于x的方程x2-px+p+3=0的两个实数根,
∴△=p2-4×1×(p+3)=0,
解得:p1=6,p2=-2(不符合题意,舍去),
则方程为x2-6x+9=0,
即AC=BD=3,
由勾股定理得:AB2+BC2=AC2=9,
∵S=
| 1 |
| 2 |
∴S≤
| 1 |
| 2 |
| 9 |
| 2 |
故答案为:
| 9 |
| 2 |
点评:本题考查了矩形的性质,勾股定理,解一元二次方程,一元二次方程的根的判别式的应用,解此题的关键是得出S≤
AC×BD.
| 1 |
| 2 |

练习册系列答案
相关题目
2014年NBA(美国男子篮球职业联赛)全明星赛中,东部明星队与西部明星队全场总分及各节得分的方差如表,由上述信息可知( )
| A | 全场得分 | 各节得分方差 | 各节得分极差 |
| 东部明星队 | 163 | 21.75 | 8 |
| 西部明星队 | 155 | 41.25 | 16 |
| A、东部明星队各节得分更稳定 |
| B、西部明星队各节得分更稳定 |
| C、两个球队各节得分一样稳定 |
| D、无法确定哪个球队各节得分更稳定 |
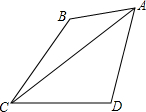 如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.
如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.