题目内容
长为2cm,3cm,4cm,5cm的四条线段,从中任取三条线段能组成三角形的概率是( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
考点:概率公式,三角形三边关系
专题:
分析:根据三角形的三边关系求出共有几种情况,根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
解答:解:∵长度为2cm、3cm、4cm、5cm的四条线段,从中任取三条线段共有C43=4种情况,
而能组成三角形的有2、3、4;3、4、5;2、4、5共有3种情况,
所以能组成三角形的概率是
,
故选C.
而能组成三角形的有2、3、4;3、4、5;2、4、5共有3种情况,
所以能组成三角形的概率是
| 3 |
| 4 |
故选C.
点评:此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
相关题目
下列方程中,无实数根的方程是( )
| A、x2-3x+2=0 | ||
| B、(x-3)2+2=x2 | ||
C、
| ||
D、
|
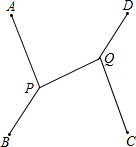 A、B、C、D四个城市恰好为一个正方形的四个顶点,要建立一个公路系统,使每两个城市之间都有公路相通,并使整个公路系统的总长为最小,则这个公路系统应当如何修建?
A、B、C、D四个城市恰好为一个正方形的四个顶点,要建立一个公路系统,使每两个城市之间都有公路相通,并使整个公路系统的总长为最小,则这个公路系统应当如何修建?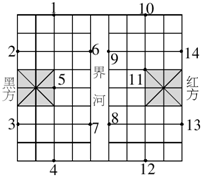 如图,这是一个中国象棋盘,图中小方格都是相同的正方形(“界河”的宽等于小正方形的边长),假设黑方只有一个“象”,它只能在1,2,3,4,5,6,7位置中的一个,红方有两个“相”,它们只能在8,9,10,11,12,13,14中的两个位置,问:这三个棋子(一个“象”和两个“相”)各在什么位置时,以这三个棋子为顶点构成的三角形的面积最大?
如图,这是一个中国象棋盘,图中小方格都是相同的正方形(“界河”的宽等于小正方形的边长),假设黑方只有一个“象”,它只能在1,2,3,4,5,6,7位置中的一个,红方有两个“相”,它们只能在8,9,10,11,12,13,14中的两个位置,问:这三个棋子(一个“象”和两个“相”)各在什么位置时,以这三个棋子为顶点构成的三角形的面积最大?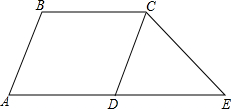 如图,在平行四边形ABCD中,点E在AD的延长线上,DE=AD,设
如图,在平行四边形ABCD中,点E在AD的延长线上,DE=AD,设