题目内容
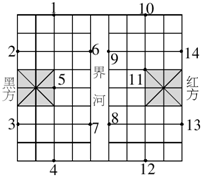 如图,这是一个中国象棋盘,图中小方格都是相同的正方形(“界河”的宽等于小正方形的边长),假设黑方只有一个“象”,它只能在1,2,3,4,5,6,7位置中的一个,红方有两个“相”,它们只能在8,9,10,11,12,13,14中的两个位置,问:这三个棋子(一个“象”和两个“相”)各在什么位置时,以这三个棋子为顶点构成的三角形的面积最大?
如图,这是一个中国象棋盘,图中小方格都是相同的正方形(“界河”的宽等于小正方形的边长),假设黑方只有一个“象”,它只能在1,2,3,4,5,6,7位置中的一个,红方有两个“相”,它们只能在8,9,10,11,12,13,14中的两个位置,问:这三个棋子(一个“象”和两个“相”)各在什么位置时,以这三个棋子为顶点构成的三角形的面积最大?考点:面积及等积变换
专题:
分析:要在这些三角形中寻求最大者,只要比较它们顶点所在边构成的三角形面积寻找最大者就可以,进而分别求出比较即可.
解答:解:我们设每个小方格的边长为1个单位,则每个小方格正方形面积为1平方厘米.
由于三个顶点都在长方形边上的三角形的面积至多为这个长方形面积的一半,
所以要在这些三角形中寻求最大者,只要比较它们顶点所在边构成的三角形面积寻找最大者就可以了.
直观可见,只需比较(3,10,12)或(2,10,12)与(3,10,13)或(2,12,14)这两类三角形的面积.
顶点为(3,10,12)或(2,10,12)的三角形面积为8×7×0.5=28;(8分)
顶点为(3,10,13)或(2,12,14)的三角形面积为9×6×0.5=27;(16分)
所以顶点在(3,10,12)或(2,10,12)时三角形的面积最大.(20分)
由于三个顶点都在长方形边上的三角形的面积至多为这个长方形面积的一半,
所以要在这些三角形中寻求最大者,只要比较它们顶点所在边构成的三角形面积寻找最大者就可以了.
直观可见,只需比较(3,10,12)或(2,10,12)与(3,10,13)或(2,12,14)这两类三角形的面积.
顶点为(3,10,12)或(2,10,12)的三角形面积为8×7×0.5=28;(8分)
顶点为(3,10,13)或(2,12,14)的三角形面积为9×6×0.5=27;(16分)
所以顶点在(3,10,12)或(2,10,12)时三角形的面积最大.(20分)
点评:此题主要考查了面积及等积变换,根据已知得出比较(3,10,12)或(2,10,12)与(3,10,13)或(2,12,14)这两类三角形的面积是解题关键.

练习册系列答案
相关题目
一张纸片,第一次把它撕成6片,第二次把其中一片又撕成6片,…,如此下去,则第n次撕后一共有小纸片数是( )
| A、6n | B、6n+1 |
| C、5n | D、5n+1 |
下列结论正确的是( )
| A、对角线相等且一组对角相等的四边形是平行四边形 |
| B、一边长为5cm,两条对角线长分别是4cm和6cm的四边形是平行四边形 |
| C、一组对边平行且一组对角相等的四边形是平行四边形 |
| D、对角线相等的四边形是平行四边形 |
长为2cm,3cm,4cm,5cm的四条线段,从中任取三条线段能组成三角形的概率是( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
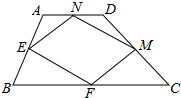
 如图,BD,CE是△ABC的两条高,F和G分别是DE和BC的中点,O是△ABC的外心.求证:AO∥FG.
如图,BD,CE是△ABC的两条高,F和G分别是DE和BC的中点,O是△ABC的外心.求证:AO∥FG.