题目内容
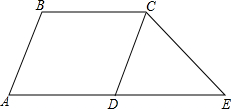如图，在平行四边形ABCD中，点E在AD的延长线上，DE=AD，设| AB |
| a |
| BC |
| b |
（1）试用向量
| a |
| b |
| CD |
| EC |
（2）求作：
| BA |
| BC |
| EC |
. |
| EC |
考点：*平面向量
专题：作图题
分析：（1）根据图形可得：
=-
，
=
=
，再由
=
+
即可得出答案．
（2）
-
=
，连接CA即可，延长AB、EC交于一点F，则可证明EF=2EC，从而可得出
+
．
| CD |
| AB |
| DE |
| AD |
| BC |
| EC |
| ED |
| DC |
（2）
| BA |
| BC |
| CA |
| EC |
. |
| EC |
解答：解：（1）由题意得，
=-
，
=
=
，
故可得：
=-
，
=
+
=-
+
．
（2）连接AC，则
-
=
；
延长AB、EC交于一点F，
由题意得，BC=AD=DE，
故可得BC=
AE，
又∵BC∥AE，
∴BC是△FAE的中位线，
∴EC=CF，
故
+
=
．
| CD |
| AB |
| DE |
| AD |
| BC |
故可得：
| CD |
| a |
| EC |
| ED |
| DC |
| b |
| a |
（2）连接AC，则
| BA |
| BC |
| CA |
延长AB、EC交于一点F，
由题意得，BC=AD=DE，
故可得BC=
| 1 |
| 2 |
又∵BC∥AE，
∴BC是△FAE的中位线，
∴EC=CF，
故
| EC |
| EC |
| EF |
点评：此题考查了平面向量、平行四边形的性质及三角形的中位线定理，解答本题的关键是熟练掌握向量的加减运算，难度一般．
练习册系列答案
相关题目
长为2cm，3cm，4cm，5cm的四条线段，从中任取三条线段能组成三角形的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
| D、1 |
如图，BD，CE是△ABC的两条高，F和G分别是DE和BC的中点，O是△ABC的外心．求证：AO∥FG．
如图，AB=AC，∠ABD=60°，∠BDC=30°，若AB=BD+CD，则∠ADB=
某中学初一年级一，二班优秀学生共25人（包括三好学生、优秀干部、积极分子、进步学生）的情况分布如下表：