题目内容
12.已知|4x+3y-5|与|x-3y-4|互为相反数,则x+y=$\frac{16}{15}$.分析 利用相反数性质,以及非负数的性质求出x与y的值,即可求出x+y的值.
解答 解:根据题意得:|4x+3y-5|+|x-3y-4|=0,
∴$\left\{\begin{array}{l}{4x+3y=5①}\\{x-3y=4②}\end{array}\right.$,
①+②得:5x=9,即x=$\frac{9}{5}$,
把x=$\frac{9}{5}$代入②得:y=-$\frac{11}{15}$,
则x+y=$\frac{16}{15}$,
故答案为:$\frac{16}{15}$.
点评 此题考查了解二元一次方程组,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
7.反比例函数y=$\frac{2a-1}{x}$的图象有一支位于第一象限,则常数a的取值范围是( )
| A. | a≥$\frac{1}{2}$ | B. | a>$\frac{1}{2}$ | C. | a≤$\frac{1}{2}$ | D. | a<$\frac{1}{2}$ |
1.1.5的倒数是( )
| A. | -$\frac{3}{2}$ | B. | -$\frac{2}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
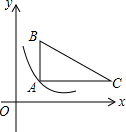 如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边AC、AB分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,AC=3.
如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边AC、AB分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,AC=3.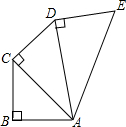 如图,AB=BC=CD=DE=1,且BC⊥AB,CD⊥AC,DE⊥AD,求线段AE的长.
如图,AB=BC=CD=DE=1,且BC⊥AB,CD⊥AC,DE⊥AD,求线段AE的长.