题目内容
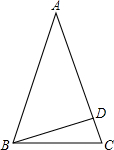如图所示，在等腰△ABC中，AB=AC=10，点D是AC边上的一点，且CD=2，BD=6．求证：∠ADB=90°．考点：勾股定理的逆定理
专题：证明题
分析：判断一组数能否成为直角三角形的三边，就是看是否满足两较小边的平方和等于最大边的平方即可．
解答：证明：∵AC=10，CD=2，
∴AD=AC-CD=8，
∵BD2+AD2=62+82=100=102=AB2，
∴△ABD是Rt△，且∠ADB=90°．
∴AD=AC-CD=8，
∵BD2+AD2=62+82=100=102=AB2，
∴△ABD是Rt△，且∠ADB=90°．
点评：本题考查了勾股定理的逆定理，判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
练习册系列答案
口算能手系列答案
相关题目
如图，GH交AB于N，交CD于P，交EF于M，PQ⊥GH交EF于Q，已知∠1=∠2=54°，∠4=36°，判断AB与EF的位置关系，并说明理由．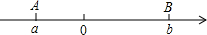
点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为AB，在数轴上A、B两点之间的距离AB=|a-b|．
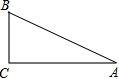在Rt△ABC中，∠C=90°，AC=4，BC=3，求sinA，sinB的值．
如图，在边长为1的小正方形组成的网络中，△ABC的三个顶点均在格点上，则cosC=
在一个边长为（已知正比例函数y=（3m+1）x的图象上有两点A（x1，y1）、B（x2，y2），当x1＜x2时，有y1＞y2，那么m的取值范围是（ ）
A、m＜-
| ||
B、m＞-
| ||
| C、m＜0 | ||
| D、m＞0 |
