题目内容
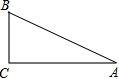在Rt△ABC中，∠C=90°，AC=4，BC=3，求sinA，sinB的值．考点：锐角三角函数的定义
专题：
分析：根据勾股定理，可得AB的长，根据在直角三角形中，锐角的正弦为对边比斜边，可得答案．
解答：解：在Rt△ABC中，∠C=90°，AC=4，BC=3，
由勾股定理，得
AB=
=
=5，
sinA=
=
，
sinB=
=
．
由勾股定理，得
AB=
| AC2+BC2 |
| 32+42 |
sinA=
| BC |
| AB |
| 3 |
| 5 |
sinB=
| AC |
| AB |
| 4 |
| 5 |
点评：本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
已知函数y=kx+b（k，b是常数，k≠0），当x＞5时，y＜0；当x＜5时，y＞0，则y=kx+b的图象必经过点（ ）
| A、（0，5） |
| B、（5，0） |
| C、（-5，0） |
| D、（0，-5） |
如图，水库大坝的横断面是梯形，坝顶宽6m，坝高23m，斜坡AB的坡度i=1：3，斜坡CD的坡度i′=1：2.5．求斜坡AB的坡角α（精确到1度），坝底宽AD和斜坡AB的长（精确到0.1m）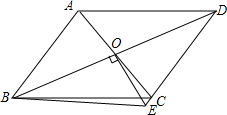
如图所示，?ABCD中，AC、BD相交于点O，OE⊥BD，交DC的延长线于E，连接BE，求证：∠ABD=∠EBD．
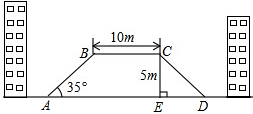如图，为了缓解交通拥堵，方便行人，在某街道计划修建一座横断面为梯形ABCD的过街天桥．天桥斜坡AB的坡角∠BAD为35°，斜坡CD的坡度为i=1：1.2（垂直高度CE与水平宽度DE的比），上底BC=10m，天桥高度CE=5m，求天桥下底AD的长度？（结果精确到0.1m，参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）
如图所示，在等腰△ABC中，AB=AC=10，点D是AC边上的一点，且CD=2，BD=6．求证：∠ADB=90°．
如图，已知CD⊥AB于D，DE⊥BC于E，∠1+∠2=90°，试说明AC⊥BC．