题目内容
10. 如图,在四边形ABCD中,∠BAE=∠ACD=90°,BC=CE.
如图,在四边形ABCD中,∠BAE=∠ACD=90°,BC=CE.(1)∠BAC与∠D相等吗?为什么?
(2)E点在AD边上,若∠BCE=90°,试判断△ACD的形状,并说明理由.
分析 (1)根据直角三角形两锐角互余可得∠CAD+∠D=90°,再根据直角可得∠BAC+∠CAD=90°,然后根据同角的余角相等解答;
(2)根据同角的余角相等求出∠ACB=∠DCE,然后利用“角角边”证明△ABC和△DEC全等,根据全等三角形对应边相等可得AC=CD,再根据等腰直角三角形的定义解答.
解答 解:(1)∠BAC=∠D.
理由如下:∵∠ACD=90°,
∴∠CAD+∠D=90°,
∵∠BAE=90°,
∴∠BAC+∠CAD=90°,
∴∠BAC=∠D;
(2)△ACD是等腰直角三角形.
理由如下:∵∠BCE=90°,
∴∠ACB+∠ACE=90°,
又∵∠ACD=90°,
∴∠DCE+∠ACE=90°,
∴∠ACB=∠DCE,
在△ABC和△DEC中,$\left\{\begin{array}{l}{∠BAC=∠D}\\{∠ACB=∠DCE}\\{BC=CE}\end{array}\right.$,
∴△ABC≌△DEC(AAS),
∴AC=CD,
又∵∠ACD=90°,
∴△ACD是等腰直角三角形.
点评 本题考查了全等三角形的判定与性质,同角的余角相等的性质,等腰直角三角形的判定,熟练掌握全等三角形的判定方法是解题的关键.

练习册系列答案
相关题目
2.为增强市民的环保意识,配合6月5日的“世界环境日”活动,某校七年级学生调查家住花园小区的50户家庭每周丢弃废塑料袋的情况,统计结果如表:
根据以上数据,若花园小区约有400户居民,则该小区所有家庭每周丢弃的废塑料袋总数为1320个.
| 每户居民丢弃废塑料袋的个数 | 1 | 2 | 3 | 4 | 5 |
| 户数 | 3 | 6 | 20 | 15 | 6 |
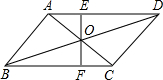 已知:?ABCD的对角线AC与BD相交于点O,过点O的直线与AD,BC分别相交于点E,F,求证:OE=OF.
已知:?ABCD的对角线AC与BD相交于点O,过点O的直线与AD,BC分别相交于点E,F,求证:OE=OF.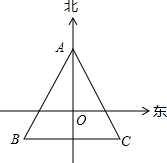 如图,等边△ABC的中心是点O,OA=3,请用OA的长与一个角度表示B、C两点的位置.
如图,等边△ABC的中心是点O,OA=3,请用OA的长与一个角度表示B、C两点的位置. 如图,点E在AC上,∠1=∠2,∠3=∠4.BE与DE相等吗?为什么?
如图,点E在AC上,∠1=∠2,∠3=∠4.BE与DE相等吗?为什么? 如图:已知AB平分∠CBD,BC=BD,试说明:AC=AD.
如图:已知AB平分∠CBD,BC=BD,试说明:AC=AD.