题目内容
12.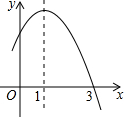 已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为x1=-1,x2=3,不等式-x2+2x+m>0的解集为-1<x<3.
已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为x1=-1,x2=3,不等式-x2+2x+m>0的解集为-1<x<3.
分析 首先把(3,0)代入二次函数y=-x2+2x+m可得m的值,然后再解-x2+2x+3=0可得解;根据二次函数y=-x2+2x+m,y>0时,图象在x轴上方可得-1<x<3,进而可得不等式-x2+2x+m>0的解集.
解答 解:根据图象可知,二次函数y=-x2+2x+m的部分图象经过点(3,0),所以该点适合方程y=-x2+2x+m,代入,得
-32+2×3+m=0,
解得m=3,
把m=3代入一元二次方程-x2+2x+m=0,得
-x2+2x+3=0,
解得x1=3,x2=-1;
∵二次函数y=-x2+2x+m,y>0时,图象在x轴上方,
∴y>0时,-1<x<3,
∴不等式-x2+2x+m>0的解集-1<x<3.
故答案为:x1=-1,x2=3;-1<x<3.
点评 本题考查的是关于二次函数与一元二次方程,在解题过程中,充分利用二次函数图象,根据图象提取有用条件来解答,这样可以降低题的难度,从而提高解题效率.

练习册系列答案
相关题目
2.“9的算术平方根”记作$\sqrt{9}$,其值是( )
| A. | 3 | B. | -3 | C. | ±3 | D. | 9 |
7.-2016的绝对值是( )
| A. | -2016 | B. | 2016 | C. | -$\frac{1}{2016}$ | D. | $\frac{1}{2016}$ |
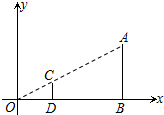 如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为$\frac{1}{3}$,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为(2,1).
如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为$\frac{1}{3}$,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为(2,1).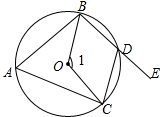 如图所示,已知四边形ABDC是圆内接四边形,∠1=112°,则∠CDE=56度.
如图所示,已知四边形ABDC是圆内接四边形,∠1=112°,则∠CDE=56度.