题目内容
4.若关于x的方程(x+1)2=k-1没有实数根,则k的取值范围是k<1.分析 通过直接开平方法解得x+1=±$\sqrt{k-1}$,则根据二次根式有意义的条件得到不等式k-1<0,由此求得k的取值范围.
解答 解:解方程(x+1)2=k-1得到:x+1=±$\sqrt{k-1}$,
∵关于x的方程(x+1)2=k-1没有实数根,
∴k-1<0,
解得:k<1.
故答案为:k<1.
点评 本题考查了解一元二次方程--直接开平方法.解题时,利用了二次根式的被开方数是非负数求得k的取值范围.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.x+2x+3x+4x+5x+…+97x+98x+99x+100x=5050,x的解是( )
| A. | 0 | B. | 1 | C. | -1 | D. | 10 |
9.把点A(-2,1)向右平移3个单位长度,再向上平移2个单位长度后得到点B,点B的坐标是( )
| A. | (1,3) | B. | (-5,3) | C. | (1,-3) | D. | (-5,-1) |
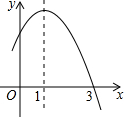 已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为x1=-1,x2=3,不等式-x2+2x+m>0的解集为-1<x<3.
已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为x1=-1,x2=3,不等式-x2+2x+m>0的解集为-1<x<3. 画图并计算:已知线段EF=30cm,延长EF到B,使FB=EF,延长FE到A,使AE=EB,求AB的长.
画图并计算:已知线段EF=30cm,延长EF到B,使FB=EF,延长FE到A,使AE=EB,求AB的长.