题目内容
14．如果$\sqrt{x+2}$=4，则$\root{3}{x+13}$=（ ）| A． | 16 | B． | 3 | C． | ±3 | D． | 14 |
分析 首先根据平方根的含义和求法，求出x的值是多少；然后根据立方根的含义和求法求解即可．
解答 解：∵$\sqrt{x+2}$=4，
∴x+2=42=16，
解得x=14，
∴$\root{3}{x+13}$
=$\root{3}{14+13}$
=$\root{3}{27}$
=3
故选：B．
点评 此题主要考查了平方根、立方根的概念的运用，要熟练掌握，解答此题的关键是求出x的值是多少．
练习册系列答案
相关题目
如图，已知线段m，n，p，求作△ABC，使AB=m，AC=n，AD=p，D为BC边上的中点，并说明理由．
19．算式（-66+$\frac{3}{17}$）×$\frac{1}{3}$可化为（ ）
| A． | -66×$\frac{1}{3}$+$\frac{3}{17}$×$\frac{1}{3}$ | B． | -66×$\frac{1}{3}$-$\frac{3}{17}$×$\frac{1}{3}$ | C． | -66×3+$\frac{3}{17}$×3 | D． | -66×3-$\frac{3}{17}$×3 |
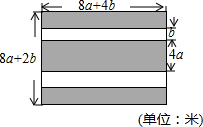2015年9月7日河北青年报报道，针对机动车数量快速增长带来的停车难等问题，住房和城乡建设都引导各城市加快编制城市停车设施专项规划，逐步缓解城市停车矛盾．某大型商超前有块长方形空地，该商场计划将此块空地修建成停车场，其设计图如图所示（阴影部分为停车位，两个小阴影部分的面积相等，空白部分为甬道，两条甬道的宽相等）