题目内容
17.(1)如图1,在正方形ABCD中,M是BC边(不含端点B,C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点,若∠AMN=90°,求证:AM=MN.(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
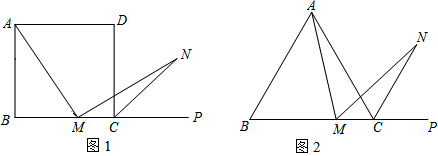
分析 (1)由题中条件可得∠AEM=∠MCN=135°,再由两角夹一边即可判定三角形全等;
(2)还是利用两角夹一边证明其全等,证明方法同(1).
解答 (1)证明:在边AB上截取AE=MC,连接ME,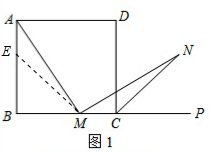
∵AE=MC,
∴BE=BM,
∴∠BEM=∠EMB=45°,
∴∠AEM=135°,
∵CN平分∠DCP,
∴∠PCN=45°,
∴∠AEM=∠MCN=135°
由三角形外角的性质可知,∠AMP=∠ABM+∠EAM,即∠AMN+∠CMN=∠ABM+∠EAM,
∵∠AMN=∠ABM=90°,
∴∠CMN=∠EAM,
在△AEM和△MCN中:
∵$\left\{\begin{array}{l}{∠AEM=∠MCN}\\{AE=CM}\\{∠EAM=∠CMN}\end{array}\right.$
∴△AEM≌△MCN,
∴AM=MN;
(2)结论:仍然成立.
证明:在边AB上截取AE=MC,连接ME,
∵△ABC是等边三角形,
∴AB=BC,∠B=∠ACB=60°,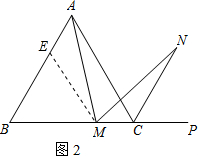
∴∠ACP=120°,
∵AE=MC,
∴BE=BM,
∴∠BEM=∠EMB=60°,
∴∠AEM=120°,
∵CN平分∠ACP,
∴∠PCN=60°,
∴∠AEM=∠MCN=120°,
∵∠CMN=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠BAM,
∴△AEM≌△MCN,
∴AM=MN.
点评 本题主要考查了全等三角形的判定及性质问题,熟练掌握其性质并能够运用所学知识证明三角形的全等问题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
14.如果$\sqrt{x+2}$=4,则$\root{3}{x+13}$=( )
| A. | 16 | B. | 3 | C. | ±3 | D. | 14 |
8. 如图,△ABC中,AD⊥BC于D,若BA=CA,则可推出△ABD≌△ACD,其依据是( )
如图,△ABC中,AD⊥BC于D,若BA=CA,则可推出△ABD≌△ACD,其依据是( )
 如图,△ABC中,AD⊥BC于D,若BA=CA,则可推出△ABD≌△ACD,其依据是( )
如图,△ABC中,AD⊥BC于D,若BA=CA,则可推出△ABD≌△ACD,其依据是( )| A. | AAS | B. | ASA | C. | SAS | D. | HL |
2. 实数a、b在数轴上的位置如图所示,正确的是( )
实数a、b在数轴上的位置如图所示,正确的是( )
 实数a、b在数轴上的位置如图所示,正确的是( )
实数a、b在数轴上的位置如图所示,正确的是( )| A. | a>-b | B. | a+b>0 | C. | ab>0 | D. | |b|<|a| |
6.填表:将x-$\frac{x}{2}$+8x2-$\frac{xyz}{3}$-$\frac{3}{5}$x2yz3中5个单项式填入下表
| 单项式 | x | -$\frac{x}{2}$ | 8x2 | -$\frac{xyz}{3}$ | -$\frac{3}{5}$x2yz3 |
| 次数 | 1 | 1 | 2 | 3 | 6 |
| 系数 | 1 | -$\frac{1}{2}$ | 8 | -$\frac{1}{3}$ | -$\frac{3}{5}$ |