Question

14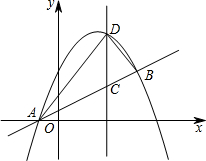．如图，抛物线y=ax²+bx+$\frac{5}{2}$与直线AB交于点A（-1，0），B（4，$\frac{5}{2}$），点D是抛物线A、B两点间部分上的一个动点（不与点A、B重合），直线CD与y轴平行，交直线AB于点C，连接AD，BD．
（1）求抛物线的表达式；
（2）设点D的横坐标为m，△ADB的面积为S，求S关于m的函数关系式，并求出当S取最大值时的点C的坐标．

Answer 1

分析 （1）将点A、B的坐标代入抛物线的解析式，求得a、b的值，从而得到抛物线的解析式；
（2）设直线AB为：y=kx+b．将A、B的坐标代入可得到k，b的方程组，从而可求得k，b于是得到直线AB的解析式，记CD与x轴的交点坐标为E．过点B作BF⊥DC，垂足为F．设D（m，-$\frac{1}{2}$m²+2m+$\frac{5}{2}$）则C（m，$\frac{1}{2}$m+$\frac{1}{2}$），依据三角形的面积公式可得到S与m的函数关系式，接下来由抛物线的对称轴方程，可求得m的值，于是可得到点C的坐标．

解答 解：（1）∵由题意得$\left\{\begin{array}{l}{a-b+\frac{5}{2}=0}\\{16a+4b+\frac{5}{2}=\frac{5}{2}}\end{array}\right.$解得：$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=2}\end{array}\right.$，
∴y=-$\frac{1}{2}$x²+2x+$\frac{5}{2}$．
（2）设直线AB为：y=kx+b．则$\left\{\begin{array}{l}{-k+b=0}\\{4k+b=\frac{5}{2}}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=\frac{1}{2}}\end{array}\right.$
直线AB的解析式为y=$\frac{1}{2}x$+$\frac{1}{2}$．
如图所示：记CD与x轴的交点坐标为E．过点B作BF⊥DC，垂足为F．

设D（m，-$\frac{1}{2}$m²+2m+$\frac{5}{2}$）则C（m，$\frac{1}{2}$m+$\frac{1}{2}$）．
∵CD=（-$\frac{1}{2}$m²+2m+$\frac{5}{2}$）-（$\frac{1}{2}$m+$\frac{1}{2}$）=$-\frac{1}{2}$m²+$\frac{3}{2}$m+2，
∴S=$\frac{1}{2}$AE•DC+$\frac{1}{2}$CD•BF=$\frac{1}{2}$CD（AE+BF）=$\frac{5}{2}$DC=$-\frac{5}{4}$m²+$\frac{15}{4}$m+5．
∴S=$-\frac{5}{4}$m²+$\frac{15}{4}$m+5．
∵-$\frac{5}{4}$＜0，
∴当m=$\frac{3}{2}$时，S有最大值．
∴当m=$\frac{3}{2}$时，$\frac{1}{2}$m+$\frac{1}{2}$=$\frac{1}{2}$×$\frac{3}{2}$+$\frac{1}{2}$=$\frac{5}{4}$．
∴点C（$\frac{3}{2}$，$\frac{5}{4}$）．

点评 本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求一次函数、二次函数的解析式、三角形的面积公式、二次函数的性质，用含m的式子表示出CD的长，从而得到S与m的关系式是解题的关键．