题目内容
1. 如图,直线AB、CD相交于O点,∠AOC=80°,OE⊥AB,OF平分∠DOB,求∠EOF的度数.
如图,直线AB、CD相交于O点,∠AOC=80°,OE⊥AB,OF平分∠DOB,求∠EOF的度数.
分析 根据对顶角得出∠BOD=∠AOC=80°,根据角平分线定义求出∠DOF=$\frac{1}{2}$∠DOB=40°,求出∠AOE=90°,求出∠EOD=10°,代入∠EOF=∠EOD+∠DOF求出即可.
解答 解:∵∠AOC=80°,
∴∠BOD=∠AOC=80°,
∵OF平分∠DOB,
∴∠DOF=$\frac{1}{2}$∠DOB=40°,
∵OE⊥AB,
∴∠AOE=90°,
∵∠AOC=80°,
∴∠EOD=180°-90°-80°=10°,
∴∠EOF=∠EOD+∠DOF=10°+40°=50°.
点评 本题考查了垂直定义,邻补角、对顶角等知识点,能求出∠DOE和∠DOF的度数是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.下列运算正确的是( )
| A. | 3a-a=2 | B. | a•a2=a3 | C. | a6÷a3=a2 | D. | (a3)2=a5 |
9.2017年2月27日在南陵县第十七届人民代表大会第一次会议上,徐晓明县长在政府工作报告中说南陵五年来,综合经济实力大幅跃升,地区生产总值增加到205.5亿元.其中205.5亿用科学记数法表示为( )
| A. | 205.5×104 | B. | 2.055×102 | C. | 2.055×1010 | D. | 2.055×1011 |
1.如图,∠1和∠2是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
 已知,如图,直线a∥b,则∠1、∠2、∠3、∠4之间的数量关系为∠1+∠4=∠2+∠3.
已知,如图,直线a∥b,则∠1、∠2、∠3、∠4之间的数量关系为∠1+∠4=∠2+∠3.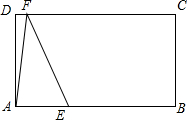 在矩形ABCD中,AB=6,AD=2$\sqrt{3}$,E是AB边上一点,AE=2,F是直线CD上一动点,将△AEF沿直线EF折叠,点A的对应点为点A′,当点E、A′、C三点在一条直线上时,DF的长度为6+2$\sqrt{7}$或6-2$\sqrt{7}$.
在矩形ABCD中,AB=6,AD=2$\sqrt{3}$,E是AB边上一点,AE=2,F是直线CD上一动点,将△AEF沿直线EF折叠,点A的对应点为点A′,当点E、A′、C三点在一条直线上时,DF的长度为6+2$\sqrt{7}$或6-2$\sqrt{7}$. 如图,若四边形ABCD是平行四边形,E、F分别是AB,AD边上的点,DE与CF交于点G,若E为AB的中点,AF=2FD,求$\frac{DG}{EG}+\frac{CG}{FG}$的值.
如图,若四边形ABCD是平行四边形,E、F分别是AB,AD边上的点,DE与CF交于点G,若E为AB的中点,AF=2FD,求$\frac{DG}{EG}+\frac{CG}{FG}$的值.