题目内容
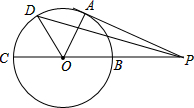 如图,PA切⊙O于点A,PO交⊙O于B,延长PO交⊙O于C,OB=PB=1,OA绕点O逆时针方向旋转60°到OD,则PD的长为
如图,PA切⊙O于点A,PO交⊙O于B,延长PO交⊙O于C,OB=PB=1,OA绕点O逆时针方向旋转60°到OD,则PD的长为考点:切线的性质
专题:
分析:由OB=PB=OA=1,可知∠OPA=30°,则∠AOB=60°,结合旋转可知∠DOC=60°,可得CD=OC=1,且PC=3,过D作DE⊥PC于点E,可求得DE=
,CE=
,可求得PE,Rt△PED中由勾股定理可求得PD.
| ||
| 2 |
| 1 |
| 2 |
解答: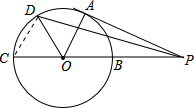 解:连接CD,
解:连接CD,
∵BC为直径,
∴∠CDP=90°,
∵PA为切线,
∴OA⊥PA,
∴∠OAP=90°
∵OA=OB=PB=1,
∴∠OPA=30°,
∴∠AOB=60°,
∵OA绕点O逆时针方向旋转60°到OD,
∴∠AOD=60°,
∴∠COD=60°,
∴△COD为等边三角形,
∴CD=CO=1,
过D作DE⊥PC于点E,则DE=
,CE=
,
∴PE=PC-CE=3-
=
,
在Rt△PCD中,PE=
,DE=
,
由勾股定理可求得PD=
=
=
.
故答案为:
.
 解:连接CD,
解:连接CD,∵BC为直径,
∴∠CDP=90°,
∵PA为切线,
∴OA⊥PA,
∴∠OAP=90°
∵OA=OB=PB=1,
∴∠OPA=30°,
∴∠AOB=60°,
∵OA绕点O逆时针方向旋转60°到OD,
∴∠AOD=60°,
∴∠COD=60°,
∴△COD为等边三角形,
∴CD=CO=1,
过D作DE⊥PC于点E,则DE=
| ||
| 2 |
| 1 |
| 2 |
∴PE=PC-CE=3-
| 1 |
| 2 |
| 5 |
| 2 |
在Rt△PCD中,PE=
| 5 |
| 2 |
| ||
| 2 |
由勾股定理可求得PD=
| DE2+PE2 |
(
|
| 7 |
故答案为:
| 7 |
点评:本题主要考查切线的性质及直角三角形的性质,在解题中证得△COD为等边三角形是解题的关键.

练习册系列答案
相关题目
在平面直角坐标系中,已知点A(-1,2)和点B(-1,0),则直线AB( )
| A、平行于x轴 |
| B、平行于y轴 |
| C、与坐标轴有2个交点 |
| D、过原点 |
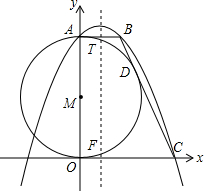 如图,在直角坐标系中,⊙M的圆心在y轴的正半轴上,AB与⊙M相切于A,BC与⊙M相切于点D,圆M与x轴相切于点O,已知B点坐标为(4,12).
如图,在直角坐标系中,⊙M的圆心在y轴的正半轴上,AB与⊙M相切于A,BC与⊙M相切于点D,圆M与x轴相切于点O,已知B点坐标为(4,12).
 如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,sinB=
如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,sinB=