题目内容
二次函数y=ax2+bx+c(a>0)的图象与x轴有两个交点A(-1,0),B(n,0),交y轴于点C(0,p),已知p=-3a(n-2).
(1)求点B的坐标;
(2)若抛物线上存在点M,且△ABM为直角三角形,求a的取值范围.
(1)求点B的坐标;
(2)若抛物线上存在点M,且△ABM为直角三角形,求a的取值范围.
考点:抛物线与x轴的交点
专题:
分析:(1)把点A、B、C的坐标分别代入函数解析式,结合p=-3a(n-2)来求系数的值;
(2)由(1)可以求得该抛物线的解析式为y=a(x+1)(x-3).由抛物线的形状可知,如果△ABM为直角三角形,那么直角顶点只能是点M.过M点作MN⊥AB于N,由△AMN∽△MBN,得出MN2=AN•BN,由此列出方程a2(x2-2x-3)2=(x+1)(x-3),通过该方程的根的判别式大于零列出关于a的不等式,通过解不等式求得a的取值范围.
(2)由(1)可以求得该抛物线的解析式为y=a(x+1)(x-3).由抛物线的形状可知,如果△ABM为直角三角形,那么直角顶点只能是点M.过M点作MN⊥AB于N,由△AMN∽△MBN,得出MN2=AN•BN,由此列出方程a2(x2-2x-3)2=(x+1)(x-3),通过该方程的根的判别式大于零列出关于a的不等式,通过解不等式求得a的取值范围.
解答: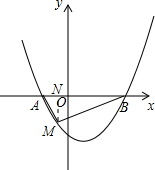 解:(1)∵二次函数y=ax2+bx+c(a>0)的图象与x轴有两个交点A(-1,0),B(n,0),交y轴于点C(0,p),p=-3a(n-2).
解:(1)∵二次函数y=ax2+bx+c(a>0)的图象与x轴有两个交点A(-1,0),B(n,0),交y轴于点C(0,p),p=-3a(n-2).
∴
,
消元,得
-2n2a+4na+6a=0,即-2a(n-3)(n+1)=0.
∵a≠0,
∴n=3或n=-1(不合题意,舍去).
∴点B的坐标是(3,0).
(2)∵由(1)知,A(-1,0),B(3,0).
∴该抛物线的解析式为y=a(x+1)(x-3).
由抛物线的形状可知,如果△ABM为直角三角形,那么直角顶点只能是点M,且点M在x轴下方.
设M点的横坐标为x,过M点作MN⊥AB于N,如图.
在△AMN与△MBN中,
∵∠ANM=∠MNB=90°,∠AMN=∠MBN=90°-∠BMN,
∴△AMN∽△MBN,
∴
=
,
∴MN2=AN•BN、
∵即a2(x2-2x-3)2=(x+1)(3-x),
整理得x2-2x-3+
=0,
∴△=4-4×(3-
)>0,
解得
<a<
,
∵a>0,
∴0<a<
.
 解:(1)∵二次函数y=ax2+bx+c(a>0)的图象与x轴有两个交点A(-1,0),B(n,0),交y轴于点C(0,p),p=-3a(n-2).
解:(1)∵二次函数y=ax2+bx+c(a>0)的图象与x轴有两个交点A(-1,0),B(n,0),交y轴于点C(0,p),p=-3a(n-2).∴
|
消元,得
-2n2a+4na+6a=0,即-2a(n-3)(n+1)=0.
∵a≠0,
∴n=3或n=-1(不合题意,舍去).
∴点B的坐标是(3,0).
(2)∵由(1)知,A(-1,0),B(3,0).
∴该抛物线的解析式为y=a(x+1)(x-3).
由抛物线的形状可知,如果△ABM为直角三角形,那么直角顶点只能是点M,且点M在x轴下方.
设M点的横坐标为x,过M点作MN⊥AB于N,如图.
在△AMN与△MBN中,
∵∠ANM=∠MNB=90°,∠AMN=∠MBN=90°-∠BMN,
∴△AMN∽△MBN,
∴
| AN |
| MN |
| MN |
| BN |
∴MN2=AN•BN、
∵即a2(x2-2x-3)2=(x+1)(3-x),
整理得x2-2x-3+
| 1 |
| a2 |
∴△=4-4×(3-
| 1 |
| a2 |
解得
| 1 |
| 2 |
| 1 |
| 2 |
∵a>0,
∴0<a<
| 1 |
| 2 |
点评:本题考查了抛物线与x轴的交点.其中涉及到的知识点有抛物线的性质,相似三角形的判定与性质,待定系数法求二次函数解析式以及两点间的坐标公式的应用,综合性较强,难度适中.

练习册系列答案
相关题目
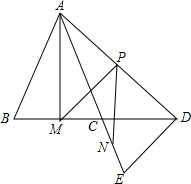 如图,已知AE与BD相交于点C,AB=AC,DE=DC,M、N、P分别是BC、CE、AD的中点.求证:
如图,已知AE与BD相交于点C,AB=AC,DE=DC,M、N、P分别是BC、CE、AD的中点.求证: 如图,D、E、F、B在一条直线上,AB=CD,∠B=∠D,BF=DE.
如图,D、E、F、B在一条直线上,AB=CD,∠B=∠D,BF=DE.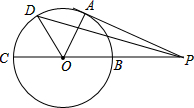 如图,PA切⊙O于点A,PO交⊙O于B,延长PO交⊙O于C,OB=PB=1,OA绕点O逆时针方向旋转60°到OD,则PD的长为
如图,PA切⊙O于点A,PO交⊙O于B,延长PO交⊙O于C,OB=PB=1,OA绕点O逆时针方向旋转60°到OD,则PD的长为