题目内容
在平面直角坐标系中，已知点A（-1，2）和点B（-1，0），则直线AB（ ）
| A、平行于x轴 |
| B、平行于y轴 |
| C、与坐标轴有2个交点 |
| D、过原点 |
考点：坐标与图形性质
专题：数形结合
分析：观察点A与点B的坐标，得到它们的横坐标相同，则可判断直线AB与x轴垂直，与y轴的距离为1个单位，所以直线AB不过原点，与坐标轴只有一个交点．
解答：解：∵点A（-1，2）和点B（-1，0），
∴直线AB与x轴垂直，
即直线是过点（-1，0）与y轴平行的直线．
故选B．
∴直线AB与x轴垂直，
即直线是过点（-1，0）与y轴平行的直线．
故选B．
点评：本题考查了坐标与图形性质：利用点的坐标计算相应的线段长和判断线段与坐标轴的位置关系．
练习册系列答案
相关题目
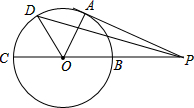如图，PA切⊙O于点A，PO交⊙O于B，延长PO交⊙O于C，OB=PB=1，OA绕点O逆时针方向旋转60°到OD，则PD的长为
如图，O是原点，有理数a，b在数轴上对应的点分别为A、B，则下列结论正确的是（ ）| A、a+b＞0 | B、2a＞0 |
| C、a-b＞0 | D、ab＜0 |
下列各式最符合代数式书写规范的是（ ）
A、2
| ||
B、
| ||
| C、3x-1个 | ||
| D、a×3 |