题目内容
在△ABC中,∠C为直角,∠A=30°,CD⊥AB于D,若BD=2,则AB的长为 .
考点:含30度角的直角三角形
专题:
分析:先根据∠ACB为直角,∠A=30°,求出∠B的度数,再根据CD⊥AB于D,求出∠DCB=30°,再利用含30度角的直角三角形的性质即可直接求出答案.
解答: 解:∵∠ACB为直角,∠A=30°,
解:∵∠ACB为直角,∠A=30°,
∴∠B=90°-∠A=60°,
∵CD⊥AB于D,
∴∠DCB=90°-∠B=30°,
∴AB=2BC,BC=2BD,
∴AB=4BD=4×2=8.
故答案为:8.
 解:∵∠ACB为直角,∠A=30°,
解:∵∠ACB为直角,∠A=30°,∴∠B=90°-∠A=60°,
∵CD⊥AB于D,
∴∠DCB=90°-∠B=30°,
∴AB=2BC,BC=2BD,
∴AB=4BD=4×2=8.
故答案为:8.
点评:此题主要考查学生对含30度角的直角三角形的性质这一知识点的理解和掌握,此题的突破点是利用∠ACB为直角和CD⊥AB于D,求出∠DCB=90°-∠B=30°,以后的问题即可迎刃而解了.

练习册系列答案
相关题目
下列各式最符合代数式书写规范的是( )
A、2
| ||
B、
| ||
| C、3x-1个 | ||
| D、a×3 |
 如图所示:已知AB=AC,补充下列条件,不能判定△ABD≌△ACD的是( )
如图所示:已知AB=AC,补充下列条件,不能判定△ABD≌△ACD的是( )| A、BD=CD |
| B、∠1=∠2 |
| C、∠3=∠4 |
| D、∠B=∠D=90° |
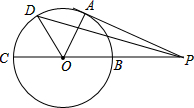 如图,PA切⊙O于点A,PO交⊙O于B,延长PO交⊙O于C,OB=PB=1,OA绕点O逆时针方向旋转60°到OD,则PD的长为
如图,PA切⊙O于点A,PO交⊙O于B,延长PO交⊙O于C,OB=PB=1,OA绕点O逆时针方向旋转60°到OD,则PD的长为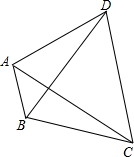 如图,已知∠ABC=120°,BD平分∠ABC,∠DAC=60°,若AB=2,BC=3,则BD的长是( )
如图,已知∠ABC=120°,BD平分∠ABC,∠DAC=60°,若AB=2,BC=3,则BD的长是( )