题目内容
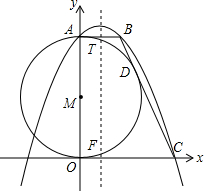 如图,在直角坐标系中,⊙M的圆心在y轴的正半轴上,AB与⊙M相切于A,BC与⊙M相切于点D,圆M与x轴相切于点O,已知B点坐标为(4,12).
如图,在直角坐标系中,⊙M的圆心在y轴的正半轴上,AB与⊙M相切于A,BC与⊙M相切于点D,圆M与x轴相切于点O,已知B点坐标为(4,12).(1)求点C的坐标;
(2)求经过A、B、C三点的函数的解析式,并写出对称轴;
(3)求圆M在抛物线的对称轴上切得的弦EF的长.
考点:二次函数综合题
专题:
分析:(1)过B作BH⊥OC于H,设OC=x,由切线长定理可求出BC的长,在直角三角形BHC中,利用勾股定理可建立关于x的方程,解方程求出x的值即可求出点C的坐标;
(2)设经过A、B、C三点的函数的解析式为y=ax2+bx+c,把A、B、C三点的坐标代入解方程组即可得到抛物线的解析式,利用公式法即可求出抛物线的对称轴;
(3)过M作MN⊥EF于N,由抛物线的对称轴可得MN的长,又因为圆的半径已知,所以利用勾股定理可求出NF的长,再根据垂径定理即可求出EF的长.
(2)设经过A、B、C三点的函数的解析式为y=ax2+bx+c,把A、B、C三点的坐标代入解方程组即可得到抛物线的解析式,利用公式法即可求出抛物线的对称轴;
(3)过M作MN⊥EF于N,由抛物线的对称轴可得MN的长,又因为圆的半径已知,所以利用勾股定理可求出NF的长,再根据垂径定理即可求出EF的长.
解答:解:(1)过B作BH⊥OC于H,设OC=x,
∵AB与⊙M相切于A,BC与⊙M相切于点D,圆M与x轴相切于点O,
∴AB=BD,OC=DC,
∵知B点坐标为(4,12),
∴OH=AB=4,AO=BH=12,
∴CH=OC-OH=x-4,BC=BD+CD=x+4,
在Rt△BHC中,BH2+CH2=BC2,
∴122+(x-4)2=(x+4)2,
解得:x=9,
∴OC=9,
即点C的坐标是(9,0);
(2)设经过A、B、C三点的函数的解析式为y=ax2+bx+c,
∵A(0,12),B(4,12),C(9,0)
∴
,
解得:
,
∴y=-
x2+
x+12,
∴抛物线对称轴是直线x=-
=2;
(3)过M作MN⊥EF于N,
∵抛物线对称轴是直线x=2,
∴MN=2,
∵MF=6,
∴NF=
=4
,
∴EF=2NF=8
.
∵AB与⊙M相切于A,BC与⊙M相切于点D,圆M与x轴相切于点O,
∴AB=BD,OC=DC,
∵知B点坐标为(4,12),
∴OH=AB=4,AO=BH=12,
∴CH=OC-OH=x-4,BC=BD+CD=x+4,
在Rt△BHC中,BH2+CH2=BC2,
∴122+(x-4)2=(x+4)2,
解得:x=9,
∴OC=9,

即点C的坐标是(9,0);
(2)设经过A、B、C三点的函数的解析式为y=ax2+bx+c,
∵A(0,12),B(4,12),C(9,0)
∴
|
解得:
|
∴y=-
| 4 |
| 15 |
| 16 |
| 15 |
∴抛物线对称轴是直线x=-
| ||
-2×
|
(3)过M作MN⊥EF于N,
∵抛物线对称轴是直线x=2,
∴MN=2,
∵MF=6,
∴NF=
| 62-22 |
| 2 |
∴EF=2NF=8
| 2 |
点评:本题着重考查了待定系数法求二次函数解析式、勾股定理的运用、垂径定理的运用以及解一元二次方程等重要知识点,综合性强,能力要求极高.考查学生计算能力,数形结合的数学思想方法.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 如图,O是原点,有理数a,b在数轴上对应的点分别为A、B,则下列结论正确的是( )
如图,O是原点,有理数a,b在数轴上对应的点分别为A、B,则下列结论正确的是( )| A、a+b>0 | B、2a>0 |
| C、a-b>0 | D、ab<0 |
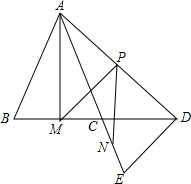 如图,已知AE与BD相交于点C,AB=AC,DE=DC,M、N、P分别是BC、CE、AD的中点.求证:
如图,已知AE与BD相交于点C,AB=AC,DE=DC,M、N、P分别是BC、CE、AD的中点.求证: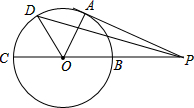 如图,PA切⊙O于点A,PO交⊙O于B,延长PO交⊙O于C,OB=PB=1,OA绕点O逆时针方向旋转60°到OD,则PD的长为
如图,PA切⊙O于点A,PO交⊙O于B,延长PO交⊙O于C,OB=PB=1,OA绕点O逆时针方向旋转60°到OD,则PD的长为