题目内容
20.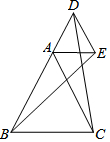 如图,已知△ABC和△ADE均为等边三角形,连接BE,CD,若∠ADC=39°,那么∠BED99度.
如图,已知△ABC和△ADE均为等边三角形,连接BE,CD,若∠ADC=39°,那么∠BED99度.
分析 只要证明△BAE≌△CAD,推出∠BEA=∠CDA=39°,即可解决问题.
解答 解:∵△ABC和△ADE均为等边三角形,
∴AB=AC,AD=AE,∠DAE=∠BAC=∠AED=60°,
∴∠BAE=∠CAD,
在△BAE和△CAD中,
$\left\{\begin{array}{l}{BA=CA}\\{∠BAE=∠CAD}\\{AE=AD}\end{array}\right.$,
∴△BAE≌△CAD,
∴∠BEA=∠CDA=39°,
∴∠BED=∠BAE+∠AED=39°+60°=99°.
故答案为99.
点评 本题考查全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 在平面直角坐标系中,已知A(0,4)、B(1,0)、C(4,0),D为线段BC上的动点,以AD为边向右侧作正方形ADEF,连CF交DE于P,则CP的最大值为1.
在平面直角坐标系中,已知A(0,4)、B(1,0)、C(4,0),D为线段BC上的动点,以AD为边向右侧作正方形ADEF,连CF交DE于P,则CP的最大值为1. 如图,已知矩形ABCD,求作⊙O,使得⊙O经过B,C两点,且与直线AD相切.(保留作图痕迹,不写作法)
如图,已知矩形ABCD,求作⊙O,使得⊙O经过B,C两点,且与直线AD相切.(保留作图痕迹,不写作法)
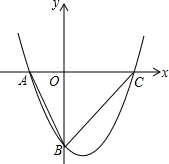 如图,抛物线y=x2-x-6交x轴于A、C两点,交y轴于点B;将抛物线y=x2-x-6向上平移$\frac{23}{4}$个单位长度、再向左平移m(m>0)个单位长度,得到新抛物线;若新抛物线的顶点P在△ABC内,则m的取值范围是0<m$<\frac{7}{3}$.
如图,抛物线y=x2-x-6交x轴于A、C两点,交y轴于点B;将抛物线y=x2-x-6向上平移$\frac{23}{4}$个单位长度、再向左平移m(m>0)个单位长度,得到新抛物线;若新抛物线的顶点P在△ABC内,则m的取值范围是0<m$<\frac{7}{3}$.