题目内容
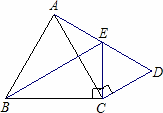
已知:如图,△BCE、△ACD分别是以BE、AD为斜边的直角三角形,且BE=AD,△CDE是等边三角形.求证:△ABC是等边三角形.
详解:∵△CDE是等边三角形,
∴EC=CD,∠1=60°.
∵BE、AD都是斜边,
∴∠BCE=∠ACD=90°
在Rt△BCE和Rt△ACD中,
EC=DC,BE=AD
∴Rt△BCE≌Rt△ACD(HL).
∴BC=AC.
 ∵∠1+∠2=90°,∠3+∠2=9
∵∠1+∠2=90°,∠3+∠2=9
 0°,
0°,
∴∠3=∠1=60°.
∴△ABC是等边三角形.


练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
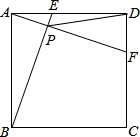

 一个三角形一定是等边三角形
一个三角形一定是等边三角形 D.4个
D.4个