题目内容
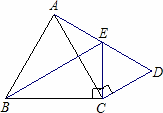
如图,正方形ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,则线段DP的最小值为__________.
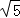 ﹣1.
﹣1.
【考点】轨迹;圆周角定理;点与圆的位置关系.
【分析】首先判断出△ABE≌△DAF,即可判断出∠DAF=∠ABE,再根据∠ABE+∠BEA=90°,可得∠FAD+∠BEA=90°,所以∠APB=90°;然后根据点P在运动中保持∠APB=90°,可得点P的路径是一段以AB为直径的弧,设AB的中点为G,连接CG交弧于点P,此时CP的长度最小,最后在Rt△AGD中,根据勾股定理,求出DG的长度,再求出PG的长度,即可求出线段DP的最小值为多少.
【解答】解:如图:
 ,
,
∵动点F,E的速度相同,
∴DF=AE,
又∵正方形ABCD中,AB=2,
∴AD=AB,
在△ABE和△DAF中,
 ,
,
∴△ABE≌△DAF,
∴∠ABE=∠DAF.
∵∠ABE+∠BEA=90°,
∴∠FAD+∠BEA=90°,
∴∠APB=90°,
∵点P在运动中保持∠APB=90°,
∴点P的路径是一段以AB为直径的弧,
设AB的中点为G,连接CG交弧于点P,此时CP的长度最小,
AG=BG=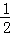 AB=1.
AB=1.
在Rt△BCG中,DG=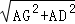 =
=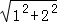 =
=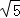 ,
,
∵PG=AG=1,
∴DP=DG﹣PG= ﹣1
﹣1
即线段DP的最小值为 ﹣1,
﹣1,
故答案为: ﹣1.
﹣1.
【点评】本题考查了轨迹,解答此题的关键是判断出什么情况下,DP的长度最小,利用了了全等三角形的判定和性质的应用,正方形的性质和应用,以及勾股定理的应用,要熟练掌握.

练习册系列答案
相关题目
 ,那么袋中的球共有__________个.
,那么袋中的球共有__________个.