题目内容
15. 金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB的高,他们在旗杆正前方台阶上的点C处,测得旗杆顶端A的仰角为45°,朝着旗杆的方向走到台阶下的点F处,测得旗杆顶端A的仰角为60°,已知升旗台的高度BE为1米,点C距地面的高度CD为3米,台阶CF的坡角为30°,且点E、F、D在同一条直线上,求旗杆AB的高度(计算结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB的高,他们在旗杆正前方台阶上的点C处,测得旗杆顶端A的仰角为45°,朝着旗杆的方向走到台阶下的点F处,测得旗杆顶端A的仰角为60°,已知升旗台的高度BE为1米,点C距地面的高度CD为3米,台阶CF的坡角为30°,且点E、F、D在同一条直线上,求旗杆AB的高度(计算结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
分析 过点C作CM⊥AB于M.则四边形MEDC是矩形,设EF=x,根据AM=DE,列出方程即可解决问题.
解答 解:过点C作CM⊥AB于M.则四边形MEDC是矩形,
∴ME=DC=3.CM=ED,
在Rt△AEF中,∠AFE=60°,设EF=x,则AF=2x,AE=$\sqrt{3}$x,
在Rt△FCD中,CD=3,∠CFD=30°,
∴DF=3$\sqrt{3}$,
在Rt△AMC中,∠ACM=45°,
∴∠MAC=∠ACM=45°,
∴MA=MC,
∵ED=CM,
∴AM=ED,
∵AM=AE-ME,ED=EF+DF,
∴$\sqrt{3}$x-3=x+3$\sqrt{3}$,
∴x=6+3$\sqrt{3}$,
∴AE=$\sqrt{3}$(6+3$\sqrt{3}$)=6$\sqrt{3}$+9,
∴AB=AE-BE=9+6$\sqrt{3}$-1≈18.4米.
答:旗杆AB的高度约为18.4米.
点评 本题考查解直角三角形-仰角俯角问题,坡度坡角问题等知识,解题的关键是学会利用参数,构建方程解决问题,属于中考常考题型.

练习册系列答案
相关题目
5.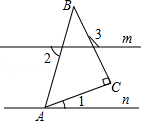 如图,直线m∥n,点A在直线n上,∠C=90°,∠1=25°,∠2=70°,则∠3的度数为( )
如图,直线m∥n,点A在直线n上,∠C=90°,∠1=25°,∠2=70°,则∠3的度数为( )
 如图,直线m∥n,点A在直线n上,∠C=90°,∠1=25°,∠2=70°,则∠3的度数为( )
如图,直线m∥n,点A在直线n上,∠C=90°,∠1=25°,∠2=70°,则∠3的度数为( )| A. | 105° | B. | 110° | C. | 115° | D. | 120° |
6. 某创意工作室6位员工的月工资如图所示,因业务需要,现决定招聘一名新员工,若新员工的工资为4500元,则下列关于现在7位员工工资的平均数和方差的说法正确的是( )
某创意工作室6位员工的月工资如图所示,因业务需要,现决定招聘一名新员工,若新员工的工资为4500元,则下列关于现在7位员工工资的平均数和方差的说法正确的是( )
 某创意工作室6位员工的月工资如图所示,因业务需要,现决定招聘一名新员工,若新员工的工资为4500元,则下列关于现在7位员工工资的平均数和方差的说法正确的是( )
某创意工作室6位员工的月工资如图所示,因业务需要,现决定招聘一名新员工,若新员工的工资为4500元,则下列关于现在7位员工工资的平均数和方差的说法正确的是( )| A. | 平均数不变,方差变大 | B. | 平均数不变,方差变小 | ||
| C. | 平均数不变,方差不变 | D. | 平均数变小,方差不变 |
3.计算:|$\sqrt{3}$-4|-$\sqrt{3}$-($\frac{1}{2}$)-2的结果是( )
| A. | 2$\sqrt{3}$-8 | B. | 0 | C. | -2$\sqrt{3}$ | D. | -8 |
11.把△ABC三条边的长度都缩小为原来的$\frac{1}{2}$,则锐角A的三角函数值( )
| A. | 也缩小为原来的$\frac{1}{2}$ | B. | 扩大为原来的2倍 | ||
| C. | 不变 | D. | 不能确定 |
