题目内容
19．计算10-（$\frac{1}{2}$）2011×（-2）2012的结果是（ ）| A． | -2 | B． | -1 | C． | 2 | D． | 3 |
分析 分别利用零指数幂的性质以及积的乘方运算法则将原式变形，进而计算得出答案．
解答 解：10-（$\frac{1}{2}$）2011×（-2）2012的
=1-[$\frac{1}{2}$×（-2）]2011×（-2）
=1-（-1）2011×（-2）
=1+1×（-2）
=-1．
故选：B．
点评 此题主要考查了零指数幂的性质以及积的乘方运算等知识，正确掌握运算法则是解题关键．
练习册系列答案
相关题目
9．
如图，AB、CD都是⊙O的弦，且AB⊥CD，若∠CDB=57°，则∠ACD的度数为（ ）
如图，AB、CD都是⊙O的弦，且AB⊥CD，若∠CDB=57°，则∠ACD的度数为（ ）| A． | 33° | B． | 34° | C． | 43° | D． | 57° |
10．下列定理中逆定理不存在的是（ ）
| A． | 全等三角形的对应角相等 | |
| B． | 如果在一个三角形中，两边相等，那么它们所对的角也相等 | |
| C． | 同位角相等，两直线平行 | |
| D． | 角平分线上的点到这个角的两边的距离相等 |
7．
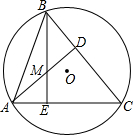如图，△ABC内接于⊙O，AD⊥BC，BE⊥AC，AD，BE相交于点M，若AC=8，BM=4，则⊙O的半径等于（ ）
如图，△ABC内接于⊙O，AD⊥BC，BE⊥AC，AD，BE相交于点M，若AC=8，BM=4，则⊙O的半径等于（ ）| A． | 2$\sqrt{5}$ | B． | 2$\sqrt{3}$ | C． | 4$\sqrt{2}$ | D． | 6 |
如图所示的几何体是由一些立方块搭成的，则这个几何体的左视图是（ ）
4．下列运算正确的是（ ）
| A． | 3x-x=2 | B． | （3x2）3=9x6 | C． | （a+2）2=a2+4 | D． | $\sqrt{27}$÷$\sqrt{3}$=3 |
11．在数-1，0，2中任取两个数作为点的坐标，那么该点刚好在一次函数y=x+2图象上的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{6}$ |
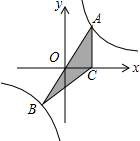如图，已知经过原点的直线AB与反比例函数y=$\frac{k}{x}$（k≠0）图象分别相交于点A和点B，过点A作AC⊥x轴于点C，若△ABC的面积为4，则k的值为（ ）
9．将点（1，-2）向右平移3个单位得到新的点的坐标为（ ）
| A． | （1，-5） | B． | （4，-2） | C． | （1，1） | D． | （-2，2） |