题目内容
7.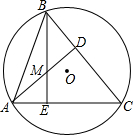 如图,△ABC内接于⊙O,AD⊥BC,BE⊥AC,AD,BE相交于点M,若AC=8,BM=4,则⊙O的半径等于( )
如图,△ABC内接于⊙O,AD⊥BC,BE⊥AC,AD,BE相交于点M,若AC=8,BM=4,则⊙O的半径等于( )| A. | 2$\sqrt{5}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{2}$ | D. | 6 |
分析 作直径AH,连接HB、HC,作OF⊥AC于F,连接CM,延长CM交AB于点N,则CN⊥AB,推出∠HCA=∠HBA=90°,证出四边形HBMC为平行四边形,求出HC,根据垂径定理求出AF,根据中位线得出OF,再根据勾股定理求出OA即可.
解答 解:作直径AH,连接HB、HC,作OF⊥AC于F,连接CM,延长CM交AB于点N,则CN⊥AB,如图所示: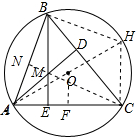
∵AH为直径,
∴∠HCA=∠HBA=90°,
∵CN⊥AB,BE⊥AC,
∴∠CNA=∠BEA=90°
∴∠HBA=∠CNA,∠HCA=∠BEA,
∴HB∥CN,HC∥BE,
∴四边形HBMC为平行四边形,
∴BM=HC=4,
∵OF⊥CC,OF过O,
∴根据垂径定理:CF=FA=$\frac{1}{2}$AC=4,
∵AO=OH,
∴OF为△ACH的中位线,
∴OF=$\frac{1}{2}$HC=2,
∴在Rt△AOF中,OA2=OF2+AF2=22+42=20,
∴AO=2$\sqrt{5}$;
故选:A.
点评 本题考查了平行四边形的判定与性质、圆周角定理、勾股定理、垂径定理、垂心定理、三角形中位线定理等知识;通过作辅助线构建平行四边形是解决问题的关键.

练习册系列答案
相关题目
17.若方程组$\left\{\begin{array}{l}{x+y=3m①}\\{x-y=7m②}\end{array}\right.$的解也是二元一次方程3x+5y=10的解,则m的值应为( )
| A. | -2 | B. | 1 | C. | $\frac{1}{2}$ | D. | 2 |
18.如图,下列图案均是长度相同的火柴并按一定的规律拼接而成:第1个图案需7根火柴,第2个图案需13根火柴,第3个图案需21根火柴,…,依此规律,第8个图案需火柴( )
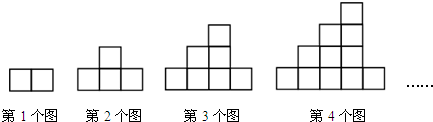

| A. | 90根 | B. | 91根 | C. | 92根 | D. | 93根 |
15.若9x2+mxy+4y2是一个完全平方式,则m的值是( )
| A. | 12 | B. | -12 | C. | ±12 | D. | ±6 |
2.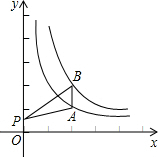 如图,点A在双曲线$y=\frac{2}{x}(x>0)$上,点B在双曲线$y=\frac{4}{x}(x>0)$上,且 AB∥y轴,点P是y轴上的任意一点,则△PAB的面积为( )
如图,点A在双曲线$y=\frac{2}{x}(x>0)$上,点B在双曲线$y=\frac{4}{x}(x>0)$上,且 AB∥y轴,点P是y轴上的任意一点,则△PAB的面积为( )
 如图,点A在双曲线$y=\frac{2}{x}(x>0)$上,点B在双曲线$y=\frac{4}{x}(x>0)$上,且 AB∥y轴,点P是y轴上的任意一点,则△PAB的面积为( )
如图,点A在双曲线$y=\frac{2}{x}(x>0)$上,点B在双曲线$y=\frac{4}{x}(x>0)$上,且 AB∥y轴,点P是y轴上的任意一点,则△PAB的面积为( )| A. | 0.5 | B. | 1 | C. | 1.5 | D. | 2 |
19.计算10-($\frac{1}{2}$)2011×(-2)2012的结果是( )
| A. | -2 | B. | -1 | C. | 2 | D. | 3 |
16.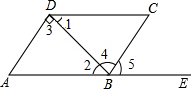 如图,四边形ABCD中,点E在AB延长线上,则下列条件中不能判断AB∥CD的是( )
如图,四边形ABCD中,点E在AB延长线上,则下列条件中不能判断AB∥CD的是( )
 如图,四边形ABCD中,点E在AB延长线上,则下列条件中不能判断AB∥CD的是( )
如图,四边形ABCD中,点E在AB延长线上,则下列条件中不能判断AB∥CD的是( )| A. | ∠3=∠4 | B. | ∠1=∠2 | C. | ∠5=∠C | D. | ∠1+∠3+∠A=180° |
17.在-$\sqrt{2}$,0,-2,1,-1这五个数中,最大的数和最小的是的和是( )
| A. | 0 | B. | -$\sqrt{2}$ | C. | -2 | D. | -1 |