题目内容
11.在数-1,0,2中任取两个数作为点的坐标,那么该点刚好在一次函数y=x+2图象上的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
分析 画树状图展示所有6种等可能的结果数,然后根据一次函数图象上点的坐标特征,找出点刚好在一次函数y=x+2图象上的结果数,再利用概率公式计算.
解答 解:画树状图为:
共有6种等可能的结果数,其中点刚好在一次函数y=x+2图象上的结果数为1,
所以该点刚好在一次函数y=x+2图象上的概率=$\frac{1}{6}$.
故选D.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了一次函数图象上点的坐标特征.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.$\sqrt{16}$等于( )
| A. | -4 | B. | 4 | C. | ±4 | D. | 256 |
2.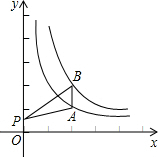 如图,点A在双曲线$y=\frac{2}{x}(x>0)$上,点B在双曲线$y=\frac{4}{x}(x>0)$上,且 AB∥y轴,点P是y轴上的任意一点,则△PAB的面积为( )
如图,点A在双曲线$y=\frac{2}{x}(x>0)$上,点B在双曲线$y=\frac{4}{x}(x>0)$上,且 AB∥y轴,点P是y轴上的任意一点,则△PAB的面积为( )
 如图,点A在双曲线$y=\frac{2}{x}(x>0)$上,点B在双曲线$y=\frac{4}{x}(x>0)$上,且 AB∥y轴,点P是y轴上的任意一点,则△PAB的面积为( )
如图,点A在双曲线$y=\frac{2}{x}(x>0)$上,点B在双曲线$y=\frac{4}{x}(x>0)$上,且 AB∥y轴,点P是y轴上的任意一点,则△PAB的面积为( )| A. | 0.5 | B. | 1 | C. | 1.5 | D. | 2 |
19.计算10-($\frac{1}{2}$)2011×(-2)2012的结果是( )
| A. | -2 | B. | -1 | C. | 2 | D. | 3 |
6.如图,填在各方格中的三个数之间均具有相同的规律,据此规律,n的值是( )


| A. | 48 | B. | 56 | C. | 63 | D. | 74 |
16.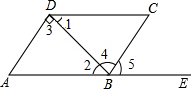 如图,四边形ABCD中,点E在AB延长线上,则下列条件中不能判断AB∥CD的是( )
如图,四边形ABCD中,点E在AB延长线上,则下列条件中不能判断AB∥CD的是( )
 如图,四边形ABCD中,点E在AB延长线上,则下列条件中不能判断AB∥CD的是( )
如图,四边形ABCD中,点E在AB延长线上,则下列条件中不能判断AB∥CD的是( )| A. | ∠3=∠4 | B. | ∠1=∠2 | C. | ∠5=∠C | D. | ∠1+∠3+∠A=180° |
20.一个解为$\left\{\begin{array}{l}x=-2\\ y=7\end{array}\right.$的二元一次方程是( )
| A. | 3x+2y=8 | B. | 3x-2y=-8 | C. | 5x+4y=-3 | D. | x+2y=1 |

 如图,已知抛物线与x轴交于A(-1,0),B(4,0),与y轴交于C(0,-2).
如图,已知抛物线与x轴交于A(-1,0),B(4,0),与y轴交于C(0,-2).