题目内容
20.计算:(1)$\sqrt{3}$($\sqrt{2}-\sqrt{3}$)-$\sqrt{24}$-|$\sqrt{6}$-3|;
(2)(3$\sqrt{18}$+$\frac{1}{5}$$\sqrt{50}$-4$\sqrt{\frac{1}{2}}$)÷$\sqrt{32}$.
分析 (1)运用乘法分配律去括号同时化简$\sqrt{24}$,根据绝对值性质去绝对值符号,再合并同类二次根式即可;
(2)先计算括号内的二次根式同时化简$\sqrt{32}$,再用二次根式的除法计算可得.
解答 解:(1)原式=$\sqrt{6}$-3-2$\sqrt{6}$-(3-$\sqrt{6}$)
=-$\sqrt{6}$-3-3+$\sqrt{6}$
=-6;
(2)原式=(9$\sqrt{2}$+$\sqrt{2}$-2$\sqrt{2}$)$÷4\sqrt{2}$
=8$\sqrt{2}$÷4$\sqrt{2}$
=2.
点评 本题考查的是二次根式的混合运算,在进行此类运算时,一般先把二次根式化为最简二次根式的形式后再运算.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
10.某市继续加大对教育经费的投入,2014年投入2500万元,2016年预计投入4000万元,假设该市投入教育经费的年平均增长率为x,根据题意列方程,则下列方程正确的是( )
| A. | 2500x2=4000 | B. | 2500(1+x%)2=4000 | ||
| C. | 2500(1+x)2=4000 | D. | 2500(1+x)+2500(1+x)2=4000 |
 如图,矩形ABCD的对角线AC、BD相交于点O,AB=4,∠AOB=60°,求对角线AC的长.
如图,矩形ABCD的对角线AC、BD相交于点O,AB=4,∠AOB=60°,求对角线AC的长.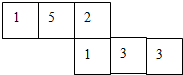 标有6个数字的立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为x,朝下一面的数字为y,得到平面直角坐标中的一个点(x,y),小敏抛掷一次立方体,则所得的点落在以坐标系原点为圆心,3为半径的圆内的概率为$\frac{1}{3}$.
标有6个数字的立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为x,朝下一面的数字为y,得到平面直角坐标中的一个点(x,y),小敏抛掷一次立方体,则所得的点落在以坐标系原点为圆心,3为半径的圆内的概率为$\frac{1}{3}$.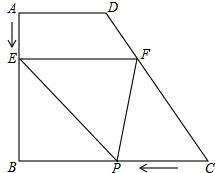 如图,四边形ABCD中,AD∥BC,∠ABC=90°,AD=6,AB=8,BC=10,直线EF从AD出发,始终保持与AD平行,并以每秒1个单位的速度向BC移动,交AB于E,交CD于F,同时点P从C点出发,沿CB方向以每秒2个单位的速度向点B移动.当P点移动到点B时,停止运动,同时直线EF也停止运动,设移动时间为t秒,连接PF、PE,△PEF的面积为S.
如图,四边形ABCD中,AD∥BC,∠ABC=90°,AD=6,AB=8,BC=10,直线EF从AD出发,始终保持与AD平行,并以每秒1个单位的速度向BC移动,交AB于E,交CD于F,同时点P从C点出发,沿CB方向以每秒2个单位的速度向点B移动.当P点移动到点B时,停止运动,同时直线EF也停止运动,设移动时间为t秒,连接PF、PE,△PEF的面积为S. 如图,AB为⊙O的直径,点C是⊙O上一点,BD切⊙O于点B,交AC的延长线于点D,点E为$\widehat{AC}$的中点,连接BE交AC于点F.
如图,AB为⊙O的直径,点C是⊙O上一点,BD切⊙O于点B,交AC的延长线于点D,点E为$\widehat{AC}$的中点,连接BE交AC于点F.