题目内容
13.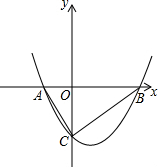 一个二次函数的图象上任一点的坐标(x,y)满足方程$\sqrt{(x-\frac{3}{2})^{2}+(y+\frac{21}{8})^{2}}$=|y+$\frac{29}{8}$|.
一个二次函数的图象上任一点的坐标(x,y)满足方程$\sqrt{(x-\frac{3}{2})^{2}+(y+\frac{21}{8})^{2}}$=|y+$\frac{29}{8}$|.(1)求此二次函数的解析式;
(2)若此二次函数与x轴的交点分别为A,B(A在B的左边),与y轴的交点为C,在此二次函数的图象上与x轴上分别找一点D,E(点D不同于点C),使得以A,D,E为顶点的三角形与△ABC相似.求出所有满足条件的点D的坐标.
分析 (1)根据等式的性质,两边平方,可得答案;
(2)根据有两个角相等的三角形相似,可得△AOC∽△ACB,△ADF与△ADE总是相似,分类讨论:①若∠DAE=∠ABC,则△AOC∽△,②若∠DAE=∠BAC,则△AOC∽△AED,根据相似三角形的性质,可得关于D点横坐标的方程,根据解方程,可得D点坐标.
解答 解:(1)两边平方得,${(x-\frac{3}{2})^2}=2y+\frac{25}{4}$
所以二次函数为$y=\frac{1}{2}{x^2}-\frac{3}{2}x-2$.
(2)令y=0,得x2-3x-4=0.
所以x1=-1,x2=4,即得A(-1,0),B(4,0).
又令x=0,得y=-2,得C(0,-2).
因为AB2=AC2+BC2.
所以△ABC是以∠ACB为直角的直角三角形.
因为∠DAE不可能为直角.
由题意可得,∠DAE=∠BAC或∠DAE=∠ABC.
作DE⊥x轴,E为垂足,设D(x0,y0),则DE=|y0|,AE=|x0+1|.
因为△AOC∽△ACB,而△ADF与△ADE总是相似的.
①若∠DAE=∠ABC,则△AOC∽△DEA,如图1: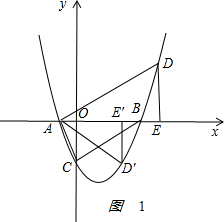 .
.
所以$\frac{AE}{OC}$=$\frac{DE}{AO}$,即$\frac{|{x}_{0}+1|}{2}$=$\frac{{|y}_{0}|}{1}$.
所以|x0+1|•|x0-4|=|x0+1|.
因为x0≠-1,所以x0=3或5.
所以D′(3,-2)或D(5,3).
②若∠DAE=∠BAC,则△AOC∽△AED,如图2: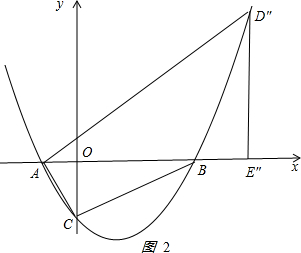 .
.
所以$\frac{AE}{AO}$=$\frac{DE}{CO}$,即$\frac{{|{x_0}+1|}}{1}=\frac{{|{y_0}|}}{2}$.
所以|x0+1|•|x0-4|=4|x0+1|.
因为x0≠-1,所以x0=0或8.
又D不同于点C,所以D″(8,18).
综上所述,点D的坐标为D′(3,-2)或D(5,3)或D″(8,18).
点评 本题考查了二次函数综合题,(1)利用了等式的性质,(2)利用了相似三角形的判定与性质,分类讨论是解题关键,以防遗漏,利用有两个角相等的三角形相似,得出△AOC∽△ACB,△ADF∽△ADE,可简便运算.

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | -22=-4 | B. | (-1)10=-10 | C. | (-$\frac{1}{3}$)3=-$\frac{1}{9}$ | D. | (-2)3=-6 |
| A. | 了解在校大学生的主要娱乐方式 | |
| B. | 了解某市居民对废电池的处理情况 | |
| C. | 日光灯管厂要检测一批灯管的使用寿命 | |
| D. | 对甲型H7N9流感患者的同一车厢的乘客进行医学检查 |
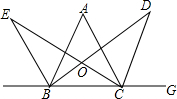 如图所示,在△ABC中,CD、BE是△ABC的外角平分线,BD为∠ABC的平分线,CE为∠ACB的平分线,BE、CE交于点E,BD、CD交于点D,试探索∠D与∠E的关系.
如图所示,在△ABC中,CD、BE是△ABC的外角平分线,BD为∠ABC的平分线,CE为∠ACB的平分线,BE、CE交于点E,BD、CD交于点D,试探索∠D与∠E的关系.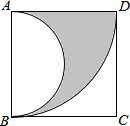 如图,在边长为4的正方形ABCD中,先以点A为圆心,AD的长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则两弧之间的阴影部分面积是2π(结果保留π).
如图,在边长为4的正方形ABCD中,先以点A为圆心,AD的长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则两弧之间的阴影部分面积是2π(结果保留π).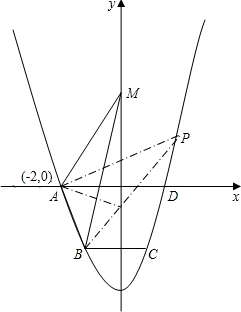 如图,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,A点到原点的距离为2,梯形的高为3,C点到y轴的距离为1,
如图,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,A点到原点的距离为2,梯形的高为3,C点到y轴的距离为1,