Question

某酒厂生产A、B两种品牌的酒，每天两种酒共生产600瓶，每种酒每瓶的成本和利润如下表所示．设每天共获利y元，每天生产A种品牌的酒x瓶．

	A	B
成本（元）	50	35
利润（元）	20	15

（1）请写出y关于x的函数关系式；

（2）如果该厂每天至少投入成本25000元，且生产B种品牌的酒不少于全天产量的55%，那么共有几种生产方案？并求出每天至少获利多少元？

Answer 1

【考点】一次函数的应用．

【分析】（1）根据获利y=A种品牌的酒的获利+B种品牌的酒的获利，即可解答．

（2）根据生产B种品牌的酒不少于全天产量的55%，A种品牌的酒的成本+B种品牌的酒的成本≥25000，列出方程组，求出x的取值范围，根据x为正整数，即可得到生产方案；再根据一次函数的性质，即可求出每天至少获利多少元．

【解答】解：（1）由题意，每天生产A种品牌的酒x瓶，则每天生产B种品牌的酒（600﹣x）瓶，

∴y=20x+15（600﹣x）=9000+5x．

（2）根据题意得：，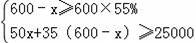

解得：266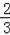≤x≤270，

∵x为整数，

∴x=267、268、269、270，

该酒厂共有4种生产方案：

①生产A种品牌的酒267瓶，B种品牌的酒333瓶；

②生产A种品牌的酒268瓶，B种品牌的酒332瓶；

③生产A种品牌的酒269瓶，B种品牌的酒331瓶；

④生产A种品牌的酒270瓶，B种品牌的酒330瓶；

∵每天获利y=9000+5x，y是关于x的一次函数，且随x的增大而增大，

∴当x=267时，y有最小值，y_最小=9000+5×267=10335元．

【点评】本题考查了一次函数的应用，关键从表格种获得成本价和利润，然后根据利润这个等量关系列解析式，根据第二问中的利润和成本做为不等量关系列不等式组分别求出解，然后根据一次函数的性质求出哪种方案获利最小．