题目内容
12.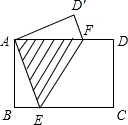 如图,长方形纸片ABCD中,AB=3cm,BC=4cm,现将A,C重合,使纸片折叠压平,设折痕为EF,试确定重叠部分△AEF的面积.
如图,长方形纸片ABCD中,AB=3cm,BC=4cm,现将A,C重合,使纸片折叠压平,设折痕为EF,试确定重叠部分△AEF的面积.
分析 要求重叠部分△AEF的面积,选择AF作为底,高就等于AB的长;而由折叠可知∠AEF=∠CEF,由平行得∠CEF=∠AFE,代换后,可知AE=AF,问题转化为在Rt△ABE中求AE.
解答 解:设AE=x,由折叠可知,EC=x,BE=4-x,
在Rt△ABE中,AB2+BE2=AE2,即32+(4-x)2=x2,
解得:x=$\frac{25}{8}$,
由折叠可知∠AEF=∠CEF,
∵AD∥BC,
∴∠CEF=∠AFE,
∴∠AEF=∠AFE,即AE=AF=$\frac{25}{8}$,
∴S△AEF=$\frac{1}{2}$×AF×AB=$\frac{1}{2}$×$\frac{25}{8}$×3=$\frac{75}{16}$.
点评 本题考查的是图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后对应角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.某班学生参加运土劳动,一部分学生抬土,另一部分学生挑土,已知全班共用箩筐99个,扁担66根,求抬土、挑土的学生各有多少人?如果设抬土的同学x人,挑土的同学y人,则可得方程组( )
| A. | $\left\{\begin{array}{l}{2(x+\frac{y}{2})=99}\\{\frac{x}{2}+y=66}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+y=66}\\{\frac{x}{2}+y=99}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{x}{2}+y=66}\\{\frac{x}{2}+2y=99}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+2y=99}\\{2x+y=66}\end{array}\right.$ |
17.一次函数y=kx-6(k<0)的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
2.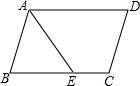 在平行四边形ABCD中,∠B=80°,AE平分∠BAD,交BC于点E,则∠AEB的度数为( )
在平行四边形ABCD中,∠B=80°,AE平分∠BAD,交BC于点E,则∠AEB的度数为( )
 在平行四边形ABCD中,∠B=80°,AE平分∠BAD,交BC于点E,则∠AEB的度数为( )
在平行四边形ABCD中,∠B=80°,AE平分∠BAD,交BC于点E,则∠AEB的度数为( )| A. | 40° | B. | 60° | C. | 50° | D. | 30° |
 把△ABC向右平移3格,再向上平移2格,画出所得到的△A′B′C,并说出线段AB与A′B′的大小及位置关系.
把△ABC向右平移3格,再向上平移2格,画出所得到的△A′B′C,并说出线段AB与A′B′的大小及位置关系. 如图,在平面直角坐标系中,直线y1=mx与双曲线y2=$\frac{k}{x}$相交于点A、B,四边形AODC为菱形,点C在x轴正半轴上,点D的坐标为(2,-3).
如图,在平面直角坐标系中,直线y1=mx与双曲线y2=$\frac{k}{x}$相交于点A、B,四边形AODC为菱形,点C在x轴正半轴上,点D的坐标为(2,-3).