题目内容
已知有一个角是30°的直角三角形,斜边为1cm,则斜边上的高为 cm.
考点:解直角三角形
专题:
分析:先根据在直角三角形中30°所对的边是斜边的一半,即可求得30°所对的直角边的长度,再利用勾股定理求得另一直角边的长度;根据角的正弦值以及另一直角边的长度即可求得斜边上的高.
解答:解:∵在直角三角形中30°所对的边是斜边的一半,
∴30°所对的直角边=
cm;
则根据勾股定理可知,另一直角边=
cm;
根据在直角三角形中30°所对的边是斜边的一半可得,
斜边上的高=
×另一直角边的长度=
cm.
故答案为:
.
∴30°所对的直角边=
| 1 |
| 2 |
则根据勾股定理可知,另一直角边=
| ||
| 2 |
根据在直角三角形中30°所对的边是斜边的一半可得,
斜边上的高=
| 1 |
| 2 |
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:本题考查了解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系.

练习册系列答案
相关题目
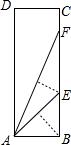 小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,则67.5°角的正切值是( )
小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,则67.5°角的正切值是( )A、
| ||
B、
| ||
| C、2.5 | ||
D、
|
在△ABC中,∠A、∠B、∠C的度数之比为3:4:5,那么△ABC是( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
 如图,AD是△ABC的中线,下列说法中,正确的是( )
如图,AD是△ABC的中线,下列说法中,正确的是( )| A、AD⊥BC |
| B、∠BAD=∠CAD |
| C、BD=CD |
| D、AD=BC |
 如图,EF为梯形ABCD的中位线,则S△ABF:S梯形ABCD=
如图,EF为梯形ABCD的中位线,则S△ABF:S梯形ABCD=