Question

9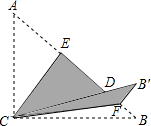．如图，Rt△ABC中，∠ACB=90°，AC=15，BC=20，将边AC沿CE翻折，使点A落在AB上的点D处，再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F，那么线段B′F的长为4．

Answer 1

分析 首先由Rt△ABC中，∠ACB=90°，AC=15，BC=20，利用勾股定理即可求得AB的长，然后由题意易得△ECF是等腰直角三角形，然后由三角形的面积公式，求得CE的长，继而求得DF的长，再利用勾股定理求得答案．

解答 解：根据折叠的性质可知：CD=AC=15，B′C=BC=20，∠ACE=∠DCE，∠BCF=∠B′CF，CE⊥AB，
∴B′D=20-15=5，∠DCE+∠B′CF=∠ACE+∠BCF，
∵∠ACB=90°，
∴∠ECF=45°，
∴△ECF是等腰直角三角形，
∴EF=CE，∠EFC=45°，
∴∠BFC=∠B′FC=135°，
∴∠B′FD=90°，
∵S_△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CE，
∴AC•BC=AB•CE，
∵根据勾股定理求得AB=25，
∴CE=12，
∴EF=12，ED=AE=$\sqrt{A{C}^{2}-C{E}^{2}}$=9，
∴DF=EF-ED=3，
∴B′F=$\sqrt{B′{D}^{2}-D{F}^{2}}$=4．
故答案为：4．

点评 此题主要考查了翻折变换，等腰三角形的判定和性质，勾股定理的应用等，根据折叠的性质求得相等的角是本题的关键．