题目内容
1.已知下列一组数:$\frac{3}{4},\frac{5}{9},\frac{7}{16},\frac{9}{25},\frac{11}{36}…$,用代数式表示第n个数,则第n个数是$\frac{1+2n}{(n+1)^{2}}$.分析 根据数列中所列的数,可以发现分子是从3开始的连续奇数,分母是序数加1的和的平方.
解答 解:∵第1个数为:$\frac{3}{4}=\frac{1+2}{{2}^{2}}$;
第2个数为:$\frac{5}{9}=\frac{1+2×2}{{3}^{2}}$;
第3个数为:$\frac{7}{16}=\frac{1+3×2}{{4}^{2}}$;
…
∴第n个数为:$\frac{1+2n}{(n+1)^{2}}$;
故答案为:$\frac{1+2n}{(n+1)^{2}}$.
点评 本题主要考查数字的变化规律,由分子、分母分别与序数的关系得出规律是关键.

练习册系列答案
相关题目
11.若y轴上的点M到x轴的距离为4,则点M的坐标是( )
| A. | (0,4) | B. | (4,0) | C. | (4,0)或(-4,0) | D. | (0,4)或(0,-4) |

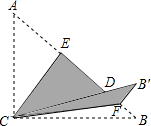 如图,Rt△ABC中,∠ACB=90°,AC=15,BC=20,将边AC沿CE翻折,使点A落在AB上的点D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,那么线段B′F的长为4.
如图,Rt△ABC中,∠ACB=90°,AC=15,BC=20,将边AC沿CE翻折,使点A落在AB上的点D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,那么线段B′F的长为4. 如图,大正方形的边长为3cm,小正方形的边长为2cm,则阴影部分的面积是2cm2.
如图,大正方形的边长为3cm,小正方形的边长为2cm,则阴影部分的面积是2cm2.