题目内容
19. 如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交于点C、点D.若DB=DC,则直线CD的函数解析式为( )
如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交于点C、点D.若DB=DC,则直线CD的函数解析式为( )| A. | y=-2x+2 | B. | y=2x-2 | C. | y=-x-2 | D. | y=-2x-2 |
分析 先求出直线AB的解析式,再根据平移的性质求直线CD的解析式.
解答 解:设直线AB的解析式为y=kx+b,
∵A(0,2)、点B(1,0)在直线AB上,
∴$\left\{\begin{array}{l}{b=2}\\{k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-2}\\{b=2}\end{array}\right.$,
∴直线AB的解析式为y=-2x+2;
∵将这直线向左平移与x轴负半轴、y轴负半轴分别交于点C、点D,使DB=DC时,平移后的图形与原图形平行,
∴平移以后的函数解析式为:y=-2x-2.
故选D.
点评 本题考查的是一次函数的图象与几何变换,熟知函数图象平移的法则是解答此题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
14.根据第六次全国人口普查数据公布,聊城市长住人口为578.99万人,常住人口数量名列全省十七地市第八名,其中578.99万人,用科学记数法表示为( )
| A. | 5.7899×105人 | B. | 5.7899×106人 | C. | 5.7899×107人 | D. | 0.57899×107人 |
11.若y轴上的点M到x轴的距离为4,则点M的坐标是( )
| A. | (0,4) | B. | (4,0) | C. | (4,0)或(-4,0) | D. | (0,4)或(0,-4) |
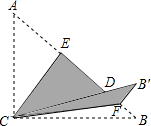 如图,Rt△ABC中,∠ACB=90°,AC=15,BC=20,将边AC沿CE翻折,使点A落在AB上的点D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,那么线段B′F的长为4.
如图,Rt△ABC中,∠ACB=90°,AC=15,BC=20,将边AC沿CE翻折,使点A落在AB上的点D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,那么线段B′F的长为4. 如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为$\frac{13}{3}$.
如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为$\frac{13}{3}$.