题目内容
20. 如图,AC与BD交于点O,AB∥DC,AB=DC.
如图,AC与BD交于点O,AB∥DC,AB=DC.(1)求证:AC与BD互相平分;
(2)若过O点作直线l,分别交AB、DC于E、F两点,求证:OE=OF.
分析 (1)由AB∥DC,根据平行线的性质,可得∠A=∠C,∠B=∠D,又由AB=DC,即可利用ASA判定△AOB≌△COD,继而证得结论;
(2)由(1),可直接利用ASA判定△AOE≌△COF,继而证得OE=OF.
解答 证明:(1)∵AB∥DC,
∴∠A=∠C,∠B=∠D,
在△AOB和△COD中,
$\left\{\begin{array}{l}{∠A=∠C}\\{AB=CD}\\{∠B=∠D}\end{array}\right.$,
∴△AOB≌△COD(ASA),
∴OA=OC,OB=OD,
即AC与BD互相平分;
(2)在△AOE和△COF中,
$\left\{\begin{array}{l}{∠A=∠C}\\{OA=OC}\\{∠AOE=∠COF}\end{array}\right.$,
∴△AOE≌△COF,
∴OE=OF.
点评 此题考查了全等三角形的判定与性质以及平行线的性质.注意利用平行线的性质,证得角相等是解此题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
8.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{\frac{2}{3}}$ | C. | $\sqrt{0.3}$ | D. | $\sqrt{11}$ |
 如图所示,△ABC为等腰三角形,∠BAC=90°,AD=AE,AF⊥BE交BC于点F,过F作FG⊥CD交BE延长线于G,GF与AC于M,求证:BG=AF+FG.
如图所示,△ABC为等腰三角形,∠BAC=90°,AD=AE,AF⊥BE交BC于点F,过F作FG⊥CD交BE延长线于G,GF与AC于M,求证:BG=AF+FG. 如图,已知AD=BC,AC=BD,求证:∠DAO=∠CBO.
如图,已知AD=BC,AC=BD,求证:∠DAO=∠CBO.

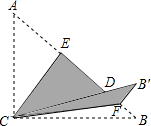 如图,Rt△ABC中,∠ACB=90°,AC=15,BC=20,将边AC沿CE翻折,使点A落在AB上的点D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,那么线段B′F的长为4.
如图,Rt△ABC中,∠ACB=90°,AC=15,BC=20,将边AC沿CE翻折,使点A落在AB上的点D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,那么线段B′F的长为4.