题目内容
13. 如图所示,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D点,OC交AB于E点.
如图所示,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D点,OC交AB于E点.(1)求∠D的度数;
(2)若CE=3,AD=4,求线段AC的长.
分析 (1)首先连接OC,由∠BAC=45°,易得△OBC是等腰直角三角形,又由AD∥OC,可求得∠D的度数;
(2)首先证得△ACE∽△DAC,然后由相似三角形的对应边成比例,求得答案.
解答 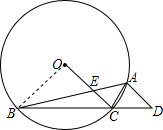 解:(1)连接OB,
解:(1)连接OB,
∵∠BOC=2∠BAC=90°,OB=OC,
∴∠OCB=∠OBC=45°,
∵AD∥OC,
∴∠D=∠OCB=45°;
(2)∵∠ABC=15°,∠OCB=45°,
∴∠AEC=60°,∠ACD=∠ABC+∠BAC=60°,
∴∠AEC=∠ACD=60°,
∵∠D=45°,∠ACD=60°,
∴∠CAD=75°,
又∵∠OCA=75°,
∴∠CAD=∠OCA=75°,
∴△ACE∽△DAC,
∴$\frac{AC}{AD}$=$\frac{CE}{AC}$,
即AC2=AD•CE=4×3=12,
∴AC=2$\sqrt{3}$.
点评 此题考查了相似三角形的判定与性质,圆周角定理,等腰三角形的性质,三角形的外角性质,以及三角形的内角和定理.注意证得△OBC是等腰直角三角形,△ACE∽△DAC是关键.

练习册系列答案
相关题目
5.如图①,边长为a的大正方形中有四个边长均为b的小正方形,小华将阴影部分拼成了一个长方形(如图②),则这个长方形的面积为( )
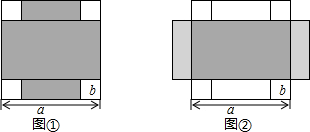

| A. | a2-4b2 | B. | (a+b)(a-b) | C. | (a+2b)(a-b) | D. | (a+b)(a-2b) |
 如图所示,正方形ABCD的边长为2,点E、F分别为边AB、AD 的中点,点G是CF上的一点,使得3CG=2GF,则三角形BEG的面积为$\frac{4}{5}$.
如图所示,正方形ABCD的边长为2,点E、F分别为边AB、AD 的中点,点G是CF上的一点,使得3CG=2GF,则三角形BEG的面积为$\frac{4}{5}$.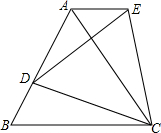 如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.
如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由. 如图所示,在边长为2的正方形ABCD的边上有一个动点P,从点A出发沿折线ABCD移动一周后,回到A点.设点A移动的路程为x,△PAC的面积为y,求函数y的解析式.
如图所示,在边长为2的正方形ABCD的边上有一个动点P,从点A出发沿折线ABCD移动一周后,回到A点.设点A移动的路程为x,△PAC的面积为y,求函数y的解析式. 沿河岸有A,B,C三个港口,甲、乙两船同时分别从A,B港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论:
沿河岸有A,B,C三个港口,甲、乙两船同时分别从A,B港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论: