题目内容
16.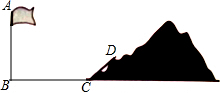 如图,学校旗杆附近有一斜坡,小明准备测量旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影子长BC=20米,斜坡坡面上的影子CD=8米,太阳光AD与水平地面BC成30°角,斜坡CD与水平地面BC成45°的角,求旗杆AB的高度.($\sqrt{3}$=1.732,$\sqrt{2}$=1.414,$\sqrt{6}$=2.449,精确到1米).
如图,学校旗杆附近有一斜坡,小明准备测量旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影子长BC=20米,斜坡坡面上的影子CD=8米,太阳光AD与水平地面BC成30°角,斜坡CD与水平地面BC成45°的角,求旗杆AB的高度.($\sqrt{3}$=1.732,$\sqrt{2}$=1.414,$\sqrt{6}$=2.449,精确到1米).
分析 延长AD交BC于E点,则BE即为AB的影长.然后根据物长和影长的比值计算即可.
解答  解:延长AD交BC于E点,则∠AEB=30°,
解:延长AD交BC于E点,则∠AEB=30°,
作DQ⊥BC于Q,
在Rt△DCQ中,∠DCQ=45°,DC=8,
∴DQ=QC=8sin45°=8×$\frac{\sqrt{2}}{2}$=4$\sqrt{2}$,
在Rt△DQE中,QE=$\frac{DQ}{tan30°}$≈9.8(米)
∴BE=BC+CQ+QE≈35.5(米)
在Rt△ABE中,AB=BEtan30°≈20(米)
答:旗杆的高度约为20米.
点评 本题查了解直角三角形的应用.解决本题的关键是作出辅助线得到AB的影长.

练习册系列答案
相关题目
11.绵阳市作为全国居民健康卡建设试点城市,尤其是在卫生信息化建设方面,绵阳市累计投入资金2亿余元,综合数据平台和卫生信息化专(兼)职队伍初步建立,其中2亿用科学记数法表示为( )
| A. | 20×108 | B. | 2×108 | C. | 0.2×108 | D. | 2×107 |
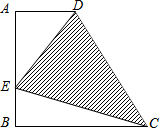 如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=BC=4,在线段AB上有一动点E.设BE=x,△DEC的面积为y,问:
如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=BC=4,在线段AB上有一动点E.设BE=x,△DEC的面积为y,问: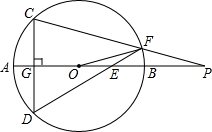 如图,已知AB是⊙O的直径,点E在线段AB上,CD⊥AB于G,连接DE交⊙O于F,连接CF交AB延长线于P.
如图,已知AB是⊙O的直径,点E在线段AB上,CD⊥AB于G,连接DE交⊙O于F,连接CF交AB延长线于P.