题目内容
7.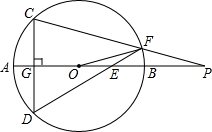 如图,已知AB是⊙O的直径,点E在线段AB上,CD⊥AB于G,连接DE交⊙O于F,连接CF交AB延长线于P.
如图,已知AB是⊙O的直径,点E在线段AB上,CD⊥AB于G,连接DE交⊙O于F,连接CF交AB延长线于P.求证:OF2=OE•OP.
分析 延长FO并交⊙O于Q,连接DQ,根据已知条件得出∠QFD+∠Q=90°和∠P+∠C=90°,再根据圆周角定理得出∠Q=∠C,求出∠QFD=∠P,从而得出△FOE∽△POF,即可得出OF2=OE•OP.
解答 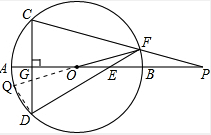 解:延长FO并交⊙O于Q,连接DQ,
解:延长FO并交⊙O于Q,连接DQ,
∵FQ是⊙O直径,
∴∠FDQ=90°,
∴∠QFD+∠Q=90°,
∵CD⊥AB,
∴∠P+∠C=90°,
∵∠Q=∠C,
∴∠QFD=∠P.
∵∠FOE=∠POF,
∴△FOE∽△POF,
∴$\frac{OE}{OF}$=$\frac{OF}{OP}$,
∴OF2=OE•OP.
点评 此题考查了相似三角形的判定与性质,用到的知识点是圆周角定理相似三角形的判定与性质,关键是根据题意求出∠QFD=∠P.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目
2.今年南方某地发生地震,政府为了尽快搭建板房安置灾民,给某厂下达了生产A种板材480002和B种板材24000m2任务.
(1)如果该厂安排210人生产这两种材,每人每天能生产A种板材60m2或B种板材40m2,请问:应分别安排多少人生产A种板材和B种板材,才能确保同时完成各自的生产任务?
(2)某灾民安置点计划用该厂上述下达任务生产的两种板材搭建甲、乙两种规格的板房共400间,已知建设一间甲型板房和一间乙型板房所需板材及安置人数如下表所示:
问:这400间板房的搭建共有多少种方案?这些方案中能最多地安置灾民的是哪一种?最多能安置灾民多少人?
(1)如果该厂安排210人生产这两种材,每人每天能生产A种板材60m2或B种板材40m2,请问:应分别安排多少人生产A种板材和B种板材,才能确保同时完成各自的生产任务?
(2)某灾民安置点计划用该厂上述下达任务生产的两种板材搭建甲、乙两种规格的板房共400间,已知建设一间甲型板房和一间乙型板房所需板材及安置人数如下表所示:
| 板房 | A种板材(m2) | B种板材(m2) | 安置人数 |
| 甲型 | 108 | 61 | 12 |
| 乙型 | 156 | 51 | 10 |
19.丹东市2014年前三季度全市实现地区生产总值855.6亿元,用科学记数法表示为( )
| A. | 855.6×108 | B. | 8.556×108 | C. | 8.556×1011 | D. | 8.556×1010 |
17.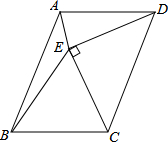 如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )
如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )
 如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )
如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )| A. | 120° | B. | 135° | C. | 150° | D. | 45° |
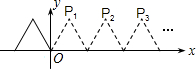 如图,将边长为2的等边三角形沿x轴正方向连续翻折2015次,依次得到点P1,P2,P3,…P2015,则点P2015的坐标是(4029,$\sqrt{3}$).
如图,将边长为2的等边三角形沿x轴正方向连续翻折2015次,依次得到点P1,P2,P3,…P2015,则点P2015的坐标是(4029,$\sqrt{3}$).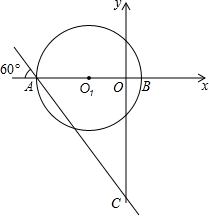 在平面直角坐标系中,点O1的坐标为(-4,0),以点O1为圆心8为半径的圆与x轴交于A,B两点.过点A作直线L与x轴负方向成60°的角,且交y轴于点C.
在平面直角坐标系中,点O1的坐标为(-4,0),以点O1为圆心8为半径的圆与x轴交于A,B两点.过点A作直线L与x轴负方向成60°的角,且交y轴于点C.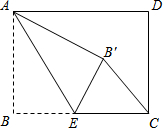 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,求BE的长.
如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,求BE的长.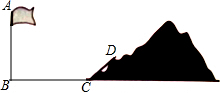 如图,学校旗杆附近有一斜坡,小明准备测量旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影子长BC=20米,斜坡坡面上的影子CD=8米,太阳光AD与水平地面BC成30°角,斜坡CD与水平地面BC成45°的角,求旗杆AB的高度.($\sqrt{3}$=1.732,$\sqrt{2}$=1.414,$\sqrt{6}$=2.449,精确到1米).
如图,学校旗杆附近有一斜坡,小明准备测量旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影子长BC=20米,斜坡坡面上的影子CD=8米,太阳光AD与水平地面BC成30°角,斜坡CD与水平地面BC成45°的角,求旗杆AB的高度.($\sqrt{3}$=1.732,$\sqrt{2}$=1.414,$\sqrt{6}$=2.449,精确到1米).