题目内容
6.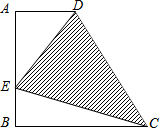 如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=BC=4,在线段AB上有一动点E.设BE=x,△DEC的面积为y,问:
如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=BC=4,在线段AB上有一动点E.设BE=x,△DEC的面积为y,问:(1)你能找出y与x的函数关系吗?(写出自变量x的取值范围)
(2)△DEC的面积可能等于5吗?说明你的理由.
(3)求出△DEC面积的最值.
分析 (1)将△DEC的面积转化为S梯形-S三角形AED-S三角形BEC,建立起y与x的函数关系式;
(2)将面积5代入(1),求出x的取值范围,若符合题意即△DEC的面积可能等于5;
(3)根据一次函数的增减性,将自变量的最大值和最小值代入解析式,可求得△DEC的面积取得最大(小)值.
解答 解:(1)设BE=x,△DEC的面积为y,由AD=2,AB=BC=4,
则:y=S梯形-S三角形AED-S三角形BEC,
=$\frac{1}{2}$×4×(2+4)-$\frac{1}{2}$×4×x-$\frac{1}{2}$(4-x)×2,
=12-2x-4+x,
=8-x,
自变量取值范围0≤x≤4,
(2)由题意可得:8-x=5,
解得:x=3,
而0<3<4,
故△DEC的面积能等于5;
(3)∵y=-x+8中,-1<0,
∴y随x的增大而减小,
当x=0时,y最大值是8,
当x=4时,y最小值是4.
点评 本题考查了一次函数的应用,将求函数解析式及其最值和图形的变化结合起来,培养了学生的数形结合的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
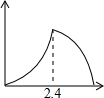
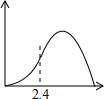
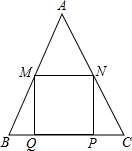 如图,锐角△ABC中,BC=6,S△ABC=12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y,则y与x的函数图象大致是( )
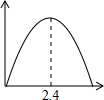
如图,锐角△ABC中,BC=6,S△ABC=12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y,则y与x的函数图象大致是( )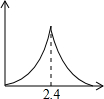
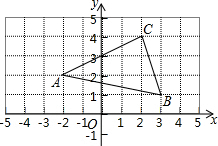 如图,在平面直角坐标系中,△ABC的各个顶点都在正方形网格的格点上,把△ABC绕点O逆时针旋转180°,得到△AB′C′,则点C′的坐标是(-2,-4).
如图,在平面直角坐标系中,△ABC的各个顶点都在正方形网格的格点上,把△ABC绕点O逆时针旋转180°,得到△AB′C′,则点C′的坐标是(-2,-4).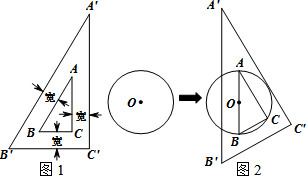
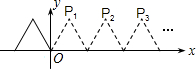 如图,将边长为2的等边三角形沿x轴正方向连续翻折2015次,依次得到点P1,P2,P3,…P2015,则点P2015的坐标是(4029,$\sqrt{3}$).
如图,将边长为2的等边三角形沿x轴正方向连续翻折2015次,依次得到点P1,P2,P3,…P2015,则点P2015的坐标是(4029,$\sqrt{3}$).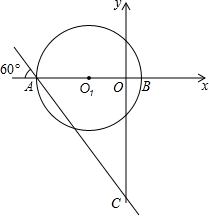 在平面直角坐标系中,点O1的坐标为(-4,0),以点O1为圆心8为半径的圆与x轴交于A,B两点.过点A作直线L与x轴负方向成60°的角,且交y轴于点C.
在平面直角坐标系中,点O1的坐标为(-4,0),以点O1为圆心8为半径的圆与x轴交于A,B两点.过点A作直线L与x轴负方向成60°的角,且交y轴于点C.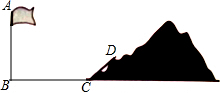 如图,学校旗杆附近有一斜坡,小明准备测量旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影子长BC=20米,斜坡坡面上的影子CD=8米,太阳光AD与水平地面BC成30°角,斜坡CD与水平地面BC成45°的角,求旗杆AB的高度.($\sqrt{3}$=1.732,$\sqrt{2}$=1.414,$\sqrt{6}$=2.449,精确到1米).
如图,学校旗杆附近有一斜坡,小明准备测量旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影子长BC=20米,斜坡坡面上的影子CD=8米,太阳光AD与水平地面BC成30°角,斜坡CD与水平地面BC成45°的角,求旗杆AB的高度.($\sqrt{3}$=1.732,$\sqrt{2}$=1.414,$\sqrt{6}$=2.449,精确到1米).