题目内容
14.(1)已知:x=2sin60°,先化简$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$+$\frac{1}{x+1}$,再求它的值.(2)已知m和n是方程3x2-8x+4=0的两根,求$\frac{1}{m}$+$\frac{1}{n}$.
分析 (1)原式第一项约分后利用同分母分式的加法法则计算得到最简结果,利用特殊角的三角函数值求出x的值,代入计算即可求出值;
(2)利用韦达定理求出m+n,mn的值,原式通分并利用同分母分式的加法法则计算,将各自的值代入计算即可求出值.
解答 解:(1)∵x=2sin60°=$\sqrt{3}$,
∴原式=$\frac{(x-1)^{2}}{(x+1)(x-1)}$+$\frac{1}{x+1}$=$\frac{x-1}{x+1}$+$\frac{1}{x+1}$=$\frac{x}{x+1}$=$\frac{\sqrt{3}}{\sqrt{3}+1}$=$\frac{3-\sqrt{3}}{2}$;
(2)∵m和n是方程3x2-8x+4=0的两根,
∴m+n=$\frac{8}{3}$,mn=$\frac{4}{3}$,
则原式=$\frac{m+n}{mn}$=2.
点评 此题考查了分式的化简求值,以及根与系数的关系,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
5. 如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( )
如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( )
 如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( )
如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( )| A. | 50° | B. | 30° | C. | 20° | D. | 15° |
2.某次列车平均提速vkm/h,用相同的时间,列车提速前行驶skm,提速后比提速前多行驶50km.设提速前列车的平均速度为xkm/h,则列方程是( )
| A. | $\frac{s}{x}$=$\frac{s+50}{x+v}$ | B. | $\frac{s}{x+v}$=$\frac{s+50}{x}$ | C. | $\frac{s}{x}$=$\frac{s+50}{x-v}$ | D. | $\frac{s}{x-v}$=$\frac{s+50}{x}$ |
9.在“青春脉动•唱响黔南校园青年歌手大赛”总决赛中,7位评委对某位选手评分为(单位:分):9、8、9、7、8、9、7.这组数据的众数和平均数分别是( )
| A. | 9、8 | B. | 9、7 | C. | 8、7 | D. | 8、8 |
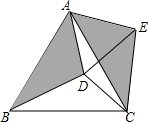 如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正切值为3$\sqrt{7}$.
如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正切值为3$\sqrt{7}$.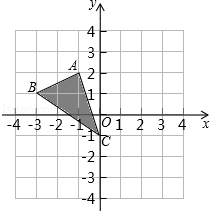 如图,已知△ABC.
如图,已知△ABC.